


: フルビッツの安定条件
: sysconh16
: 最小実現のアルゴリズム
システムの安定性は主に次の2つがある.
- 内部安定性
- システムに入力を加えない(すなわち
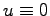 )で放置したときのシステムの状態が時間と共に
)で放置したときのシステムの状態が時間と共に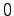 になるかどうか.
になるかどうか.
- 入出力安定性(BIBO安定性)
- ある条件(通常は有界入力条件)を満足する入力を加えた場合に,出力が有界であるかどうか.
本節では主として線形システムの内部安定性を論じる.
線形システム
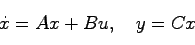 |
(15.1) |
において入力を零としたときの状態は,任意の初期値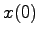 に対して
に対して
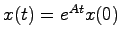 で与えられるが,この
で与えられるが,この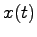 のノルム(絶対値と考えてもらって差し支えない)
のノルム(絶対値と考えてもらって差し支えない)
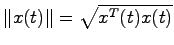 が時間の経過と共に
が時間の経過と共に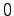 に収束するとき,システム(5.1)は漸近安定であるという.すなわち任意の初期値
に収束するとき,システム(5.1)は漸近安定であるという.すなわち任意の初期値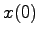 に対して
に対して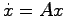 の解
の解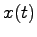 が
が
を満たすとき,システム(5.1)は漸近安定であると定義される.
上記の定義より解るように,システムの漸近安定性は のみによって定まる.
のみによって定まる.
例5.1 システム
を考える.教科書(2.22)式:
より
![\begin{displaymath}
e^{At} = {\cal L}^{-1}\left(\left[ \begin{array}{cc}
s+1 & 0...
...\begin{array}{cc}
e^{-t} & 0 0 & e^{-2t} \end{array}\right]
\end{displaymath}](img761.png) |
(15.4) |
となる.したがって零入力時のシステムの状態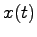 は
は
![\begin{displaymath}
x(t) = e^{At}x(0) = \left[ \begin{array}{c}
e^{-t}x_1(0) e^{-2t}x_2(0) \end{array}\right]
\end{displaymath}](img762.png) |
(15.5) |
で与えられる.よって
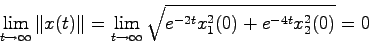 |
(15.6) |
となり,内部安定性に関して漸近安定である.
上の例から内部安定性は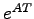 ,すなわち
,すなわち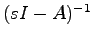 に関連しており,行列
に関連しており,行列 の固有値が漸近安定性と結びつきそうであると考えられる.これに対し次の定理が成り立つ.
の固有値が漸近安定性と結びつきそうであると考えられる.これに対し次の定理が成り立つ.
定理5.1 システム(5.1)が漸近安定であるための必要十分条件は, の特性方程式
の特性方程式
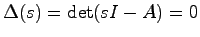 の根(すなわち
の根(すなわち の固有値)の実部がすべて負であることである.
の固有値)の実部がすべて負であることである.
証明は線形代数の知識(固有値と固有空間に関する理論)を必要とするため省略する
例5.2 システム
を考える. の特性方程式は
の特性方程式は
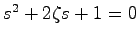 であるから,
であるから,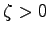 のとき,このシステムは漸近安定である.実際,零入力におけるこのシステムの状態
のとき,このシステムは漸近安定である.実際,零入力におけるこのシステムの状態
![$x=\left[x_1 \; x_2\right]^T$](img769.png) は
は
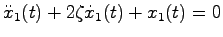 |
|
|
(15.9) |
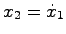 |
|
|
(15.10) |
を満足することから,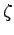 の値に応じて教科書図5.1のように,システムの安定性と共に零入力応答が変化する.
の値に応じて教科書図5.1のように,システムの安定性と共に零入力応答が変化する.
入出力安定性について 線形システム(5.1)の初期状態が零であるときに,任意の有界な入力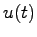 (すなわち,任意の時刻
(すなわち,任意の時刻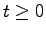 に対して
に対して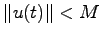 となる定数
となる定数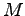 が存在する入力)に対する出力が有界であれば,このシステムは,有界入力有界出力安定であるという.このとき,システム(5.1)が有界入力有界出力安定であるための必要十分条件は,その伝達関数行列
が存在する入力)に対する出力が有界であれば,このシステムは,有界入力有界出力安定であるという.このとき,システム(5.1)が有界入力有界出力安定であるための必要十分条件は,その伝達関数行列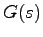 (すなわち,
(すなわち,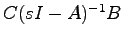 の各要素の既約形を取った行列)の各要素
の各要素の既約形を取った行列)の各要素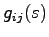 の極の実部がすべて負となることである.この条件は,1入力1出力システムの場合には,伝達関数のすべての極の実部が負であることという古典制御理論における安定性の必要十分条件に帰着される.また,システム(5.1)が可制御可観測である場合には,
の極の実部がすべて負となることである.この条件は,1入力1出力システムの場合には,伝達関数のすべての極の実部が負であることという古典制御理論における安定性の必要十分条件に帰着される.また,システム(5.1)が可制御可観測である場合には, の漸近安定性の条件と,有界入力有界出力安定性の条件は一致する.このことから
の漸近安定性の条件と,有界入力有界出力安定性の条件は一致する.このことから の固有値を,システム(5.1)の極と呼ぶ.なおシステム(5.1)が可制御可観測でない場合には,次の例からも判るように,その漸近安定性と有界入力有界出力安定性は必ずしも一致しない.
の固有値を,システム(5.1)の極と呼ぶ.なおシステム(5.1)が可制御可観測でない場合には,次の例からも判るように,その漸近安定性と有界入力有界出力安定性は必ずしも一致しない.
例5.3 システム
を考える.これは教科書図5.2のブロック線図で与えられるシステムの状態方程式である. の固有値は
の固有値は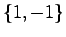 であるから,このシステムは内部安定ではない.しかし伝達関数
であるから,このシステムは内部安定ではない.しかし伝達関数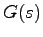 は
は
![\begin{displaymath}
G(s) = \left[ \begin{array}{cc}1 & 0 \end{array}\right]
\lef...
... 1 \end{array}\right]
= \frac{s-1}{(s+1)(s-1)} = \frac{1}{s+1}
\end{displaymath}](img779.png) |
(15.13) |
となり,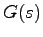 の極は
の極は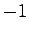 であるから有界入力有界出力安定である.
上記の結果は,図5.2の下側のブロックの状態変数
であるから有界入力有界出力安定である.
上記の結果は,図5.2の下側のブロックの状態変数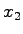 は,初期値が0でないと発散してしまう.このことはシステムの内部に不安定部分が存在することを示す.さらにこの不安定部分は入力と出力の関係には現れないことから,内部的には不安定であるが入出力関係では安定になることがわかる.
(5.18)に示したように,伝達関数を求める際に,システムの内部にある不安定な極
は,初期値が0でないと発散してしまう.このことはシステムの内部に不安定部分が存在することを示す.さらにこの不安定部分は入力と出力の関係には現れないことから,内部的には不安定であるが入出力関係では安定になることがわかる.
(5.18)に示したように,伝達関数を求める際に,システムの内部にある不安定な極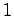 が,分母分子で消去(約分)されてしまうことに注意する.このことは以前説明したようにシステムが可観測でないこと(すなわち内部状態が観測不可能であること)に起因している.
が,分母分子で消去(約分)されてしまうことに注意する.このことは以前説明したようにシステムが可観測でないこと(すなわち内部状態が観測不可能であること)に起因している.
有界入力有界出力安定性は,ここでは古典制御理論での安定性との関係を明らかにするために取り上げた.ただ,たとえ入出力安定性の意味で安定であったとしても内部的に不安定な部分が存在することはシステム設計上好ましくない.
したがって以下では内部安定性,特に漸近安定性についておもに議論する.



: フルビッツの安定条件
: sysconh16
: 最小実現のアルゴリズム
endo
平成16年6月30日
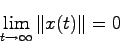
![]() のみによって定まる.
のみによって定まる.
![]() ,すなわち
,すなわち![]() に関連しており,行列
に関連しており,行列![]() の固有値が漸近安定性と結びつきそうであると考えられる.これに対し次の定理が成り立つ.
の固有値が漸近安定性と結びつきそうであると考えられる.これに対し次の定理が成り立つ.
![]() の特性方程式
の特性方程式
![]() の根(すなわち
の根(すなわち![]() の固有値)の実部がすべて負であることである.
の固有値)の実部がすべて負であることである.
![]() (すなわち,任意の時刻
(すなわち,任意の時刻![]() に対して
に対して![]() となる定数
となる定数![]() が存在する入力)に対する出力が有界であれば,このシステムは,有界入力有界出力安定であるという.このとき,システム(5.1)が有界入力有界出力安定であるための必要十分条件は,その伝達関数行列
が存在する入力)に対する出力が有界であれば,このシステムは,有界入力有界出力安定であるという.このとき,システム(5.1)が有界入力有界出力安定であるための必要十分条件は,その伝達関数行列![]() (すなわち,
(すなわち,![]() の各要素の既約形を取った行列)の各要素
の各要素の既約形を取った行列)の各要素![]() の極の実部がすべて負となることである.この条件は,1入力1出力システムの場合には,伝達関数のすべての極の実部が負であることという古典制御理論における安定性の必要十分条件に帰着される.また,システム(5.1)が可制御可観測である場合には,
の極の実部がすべて負となることである.この条件は,1入力1出力システムの場合には,伝達関数のすべての極の実部が負であることという古典制御理論における安定性の必要十分条件に帰着される.また,システム(5.1)が可制御可観測である場合には,![]() の漸近安定性の条件と,有界入力有界出力安定性の条件は一致する.このことから
の漸近安定性の条件と,有界入力有界出力安定性の条件は一致する.このことから![]() の固有値を,システム(5.1)の極と呼ぶ.なおシステム(5.1)が可制御可観測でない場合には,次の例からも判るように,その漸近安定性と有界入力有界出力安定性は必ずしも一致しない.
の固有値を,システム(5.1)の極と呼ぶ.なおシステム(5.1)が可制御可観測でない場合には,次の例からも判るように,その漸近安定性と有界入力有界出力安定性は必ずしも一致しない.
![\begin{displaymath}
G(s) = \left[ \begin{array}{cc}1 & 0 \end{array}\right]
\lef...
... 1 \end{array}\right]
= \frac{s-1}{(s+1)(s-1)} = \frac{1}{s+1}
\end{displaymath}](img779.png)