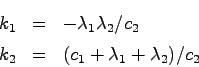: 状態フィードバックによる1入力システムの極配置
: sysconh16
: 安定性と可観測性
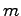 入力で
入力で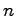 次元状態変数をもつ線形システム
次元状態変数をもつ線形システム
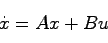 |
(20.1) |
において,状態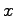 が直接計測できる場合,すなわち
が直接計測できる場合,すなわち
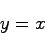 |
(20.2) |
と置ける場合を考える.このシステムの安定性,過渡応答特性などは,その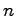 個の極の配置に大きく左右される.極と安定性の関係については前章で示したので,ここでは極と過渡応答の関係を簡単な例により示す.
個の極の配置に大きく左右される.極と安定性の関係については前章で示したので,ここでは極と過渡応答の関係を簡単な例により示す.
例6.1 システム
を考える.
ただし,
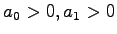 とする.このシステムの伝達関数行列は
とする.このシステムの伝達関数行列は
で与えられる.
ただし,
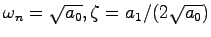 とした.したがってこのシステムの極は
とした.したがってこのシステムの極は
となる.これら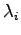 については明らかに
については明らかに
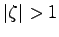 のときには
のときには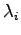 は実数
は実数
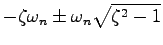 ,
,
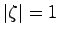 のときには
のときには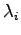 は実数の重解
は実数の重解
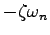 ,
,
-
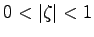 のときには
のときには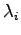 は複素数
は複素数
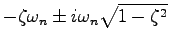 ,
,
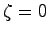 のときには
のときには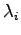 は純虚数
は純虚数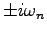
である.
また,このシステムの極配置とインディシャル応答(ステップ応答)との関係は,図6.1のようになる.図より判るように,極が複素平面上で原点から遠いほど過渡応答の速度は速く(図6.1(b)の横軸スケールが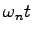 であることから,同一の
であることから,同一の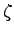 に対しても
に対しても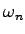 が大きいほど収束が速いことに注意),原点から見た極の位置が負の水平方向に近いほど減衰が大きい.
が大きいほど収束が速いことに注意),原点から見た極の位置が負の水平方向に近いほど減衰が大きい.
さて,システム(20.1),(20.2)に対して,線形状態フィードバック制御則
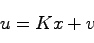 |
(20.3) |
を適用してみる.ただし,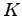 は定数フィードバックゲイン行列,
は定数フィードバックゲイン行列,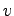 は
は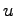 に代わる新たな制御入力である.このとき制御系全体は図6.2のようになり,閉ループ系の状態方程式は
に代わる新たな制御入力である.このとき制御系全体は図6.2のようになり,閉ループ系の状態方程式は
となる.式の形は(20.1)式と同じであるが,状態変数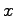 の係数行列が
の係数行列が から
から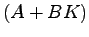 に変わっている点に注意されたい.これにより開ループ系の極が移動することから,開ループ系の極が複素平面上の望ましい位置にない場合に,制御則(20.3)などによって,閉ループ系を構成し,その極を希望する位置に配置する問題を極配置問題という.
に変わっている点に注意されたい.これにより開ループ系の極が移動することから,開ループ系の極が複素平面上の望ましい位置にない場合に,制御則(20.3)などによって,閉ループ系を構成し,その極を希望する位置に配置する問題を極配置問題という.
次に状態フィードバックによる極配置が有効であることを示す簡単な例を与える.
例6.2 電機子制御直流サーボモータについて考える.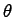 をモータの回転角とし,
をモータの回転角とし,
とおくとき,モータの状態方程式が
で与えられるものとする.ただし,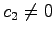 とする.
このシステムの極は
とする.
このシステムの極は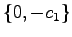 である.いま,
である.いま,
なる状態フィードバックを与えると,閉ループ系は
となり,閉ループ系の極は
の根で与えられる.よって,この極を
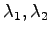 に配置したいときには
に配置したいときには
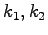 を
を
とすればよい.したがって,
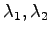 の配置を適当に決めることができ,これにより適切な応答速度と減衰をもたせることができる.
の配置を適当に決めることができ,これにより適切な応答速度と減衰をもたせることができる.
endo
平成16年6月30日
![\begin{displaymath}
\dot{x} = \left[ \begin{array}{cc}
0 & 1 -a_0 & -a_1 \end...
...t[ \begin{array}{c}
0 a_0 \end{array}\right] u, \quad y = x
\end{displaymath}](img898.png)
![\begin{eqnarray*}
G(s) &=& C(sI-A)^{-1}B
= \left[ \begin{array}{cc}
s & -1 a...
..._ns+\omega_n^2}\left[ \begin{array}{c}
1 s \end{array}\right]
\end{eqnarray*}](img900.png)
![]() をモータの回転角とし,
をモータの回転角とし,
![\begin{displaymath}
x = \left[ \begin{array}{c}\theta \dot{\theta}\end{array}\right]
\end{displaymath}](img918.png)
![\begin{displaymath}
\dot{x} = \left[ \begin{array}{cc} 0 & 1 0 & -c_1 \end{ar...
...right]x
+ \left[ \begin{array}{c}0 c_2 \end{array}\right] u
\end{displaymath}](img919.png)
![\begin{displaymath}
u = \left[ \begin{array}{cc}k_1 & k_2 \end{array}\right] x + v
\end{displaymath}](img922.png)
![\begin{displaymath}
\dot{x} = \left[ \begin{array}{cc}
0 & 1 k_1 c_2 & -c_1+k...
...ght] x + \left[ \begin{array}{c}
0 c_2 \end{array}\right] v
\end{displaymath}](img923.png)