![\includegraphics[scale=0.5]{ENERGY.eps}](img21.png)
|
まずバックプロバゲーションを理解する為にその基礎となる最急降下法についての説明を行なう。 最急降下法のイメージを図 3.1で示す。
説明する上で誤差の関数![]() (ネットワークの出力と教師信号との誤差)と結合荷重
(ネットワークの出力と教師信号との誤差)と結合荷重![]() (入力層と出力層をつなぐ荷重)を定義しておく。
最急降下法とは誤差の関数
(入力層と出力層をつなぐ荷重)を定義しておく。
最急降下法とは誤差の関数![]() が小さくなるように結合荷重
が小さくなるように結合荷重![]() を求めるための方法の一つである。
この方法は、関数のある一点の勾配を算出し、誤差
を求めるための方法の一つである。
この方法は、関数のある一点の勾配を算出し、誤差![]() が小さくなる方向に結合荷重を変化させる。
最急降下法を使用するためには、勾配を求める、
即ち微分をする必要があるため微分可能で連続である関数を準備しなければならない。
この方法には問題点があり、それが必ず誤差が一番小さくなる
が小さくなる方向に結合荷重を変化させる。
最急降下法を使用するためには、勾配を求める、
即ち微分をする必要があるため微分可能で連続である関数を準備しなければならない。
この方法には問題点があり、それが必ず誤差が一番小さくなる![]() の値にならないという事である。
実際は微分を用いるため、極小値(ローカルミニマム)に収束する。
の値にならないという事である。
実際は微分を用いるため、極小値(ローカルミニマム)に収束する。
実際にバックプロパゲーションを適応させる場合についての説明を行なう。
いくつかの中間層を持つ階層型のネットワークを考える。
同じ層の素子間に結合はなく、
どの素子も1つ前の層からのみ入力を受け、
次の層へのみ出力を送るものとする。
このようなネットワークの中間層に対して学習則を導くとき、
![]() (学習信号)の値は
すぐには求めることが出来ない。
そのため、この学習信号を出力層から逆向きに順々に計算していく。
すなわち出力の誤差を前の層へ、前の層へと伝えていく。
学習の評価基準として、次のような誤差関数
(学習信号)の値は
すぐには求めることが出来ない。
そのため、この学習信号を出力層から逆向きに順々に計算していく。
すなわち出力の誤差を前の層へ、前の層へと伝えていく。
学習の評価基準として、次のような誤差関数![]() を定義する。
を定義する。
式 3.1での![]() とはある入力
とはある入力![]() に対して出力素子
に対して出力素子![]() 出力がすべき望ましい出力、
出力がすべき望ましい出力、![]() はそのときの出力を指している。
この誤差を
はそのときの出力を指している。
この誤差を![]() について微分をすると
について微分をすると
よって、
ある層の素子 ![]() の
の
![]() の計算は、
次の層の素子
の計算は、
次の層の素子 ![]() の
の
![]() を用いて
を用いて
と展開することができる。
また、出力![]() と結合荷重
と結合荷重![]() の積和が入力総和
の積和が入力総和![]() であることから
であることから
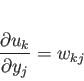 |
(3.4) |
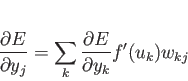 |
(3.5) |
バックプロパゲーションは、いかなる重みの初期値からでも誤差が極小となる
(最小ではない)ことが保証されるわけだが、一般に誤差曲面は
極小値の近くでは非常に緩やかな谷底をもつため、学習は非常に遅くなる。
しかし、学習係数の ![]() を大きくすると、学習は振動してしまう。
振動させずに学習を早めるため幾つかの方法が提案されているが、例えば、
誤差曲面の傾きを結合荷重空間の位置でなく速度の変化に用いる。
即ち、
を大きくすると、学習は振動してしまう。
振動させずに学習を早めるため幾つかの方法が提案されているが、例えば、
誤差曲面の傾きを結合荷重空間の位置でなく速度の変化に用いる。
即ち、
図3.2 に バックプロパゲーション法のネットワーク図を示す。 バックプロパゲーションの特徴としては、