正弦波の学習

1周期におけるサンプリング数(分割数)を

とした時、時間

における信号

を

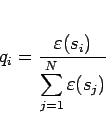$\begin{displaymath} q_i = \frac{\varepsilon(s_i)}{\displaystyle \sum_{j=1}^N \varepsilon(s_j)} \end{displaymath}$

(6.2)

時系列データの予測を行うのが目的であるので、ある時刻における正弦波の値を入力したら、次の時刻の正弦波の値を出力するのが望ましい。つまり、カオスニューロンの望ましい出力としては、入力波形の次の状態である教師信号の値を出力することである。よって、時刻

における入力信号を、6.1式の

、教師信号は $y_{i+1}$ とした。

**図 6.1:** 分割数4の正弦波を学習させた時の遺伝的アルゴリズムの評価値の推移
$\includegraphics[scale=1.0]{fig/sin/genes_gosa/gnu1-4_gene.eps}$

まず始めに、正弦波の分割数(サンプリング数)を4とした時の実験を行った。バックプロパゲーションの学習時間を

とし、この時の遺伝的アルゴリズムによる各世代のエリート遺伝子の評価値の推移を図 6.1に示す。横軸が初期集団を生成してからの世代数、縦軸が遺伝的アルゴリズムに用いた評価値である。分割数が4の場合においては、初期集団から誤差が低いもの現れ、多少ばらつきがあるが、世代数が80を過ぎた辺りから安定した誤差となった。本来はエリート選択保存を採用しているため、誤差が大きくなる様に動くことはないのだが、誤差にばらつぎがあるということは、

**図 6.2:** 分割数4の正弦波を学習させた時の最大誤差の推移
$\includegraphics[scale=1.0]{fig/sin/out_of_neuron_ck4.eps}$

この最終世代のエリート遺伝子をカオスニューロンを用いたバックプロパゲーションに適用した結果を図 6.2に示す。縦軸が正弦波一周期において、カオスニューロンが正弦波を学習して出力した値と、教師信号の値との誤差が最大となる値とした。横軸がその時の周期数(学習時間)を表す。グラフから、全体としては時間と共にネットワークの学習を進行されてるが、時間が30〜250くらいの間では誤差が大きく変動するような特性が見られる。また、段階を得て学習を進めている様にも見れる。この時の誤差の最終値は0.009398と低い値を示し、これを学習成功とする。学習成功の基準は後に述べることにする。

**図 6.3:** 分割数1から50まで変化させた時の誤差
$\includegraphics[scale=1.0]{fig/sin/clock1-50no_gosa.eps}$

次に入力波形の分割数を変化させても、同様に学習できるかどうかを調べた。分割数を1〜50まで変更させた時の結果を図 6.3に示す。

横軸が、入力波形である正弦波の分割数、縦軸がバックプロパゲーションによる遺伝的アルゴリズムへの評価値を表す。グラフを見てみると、分割数が7以降では誤差は分割数に関係なく低い値を示しており、分割数が1, 2, 3など極端に小さい時は誤差がほとんどみられなかった。分割数が11〜50においては誤差に多少のばらつきがみられるが、比較的小さい誤差を示している。

図 6.4: バックプロパゲーション終了後におけるカオスニューロンの動作(正弦波)

$\includegraphics[scale=0.6]{fig/sin/afterpro1/after1_11.eps}$	$\includegraphics[scale=0.6]{fig/sin/afterpro1/after1_13.eps}$
(a)分割数11の例	(b)分割数13の例
$\includegraphics[scale=0.6]{fig/sin/afterpro1/after1_16.eps}$	$\includegraphics[scale=0.6]{fig/sin/afterpro1/after1_21.eps}$
(c)分割数16の例	(d)分割数21の例

**表 6.1:** 各分割数におけるバックプロパゲーションによる評価値
分割数	評価値(誤差)
11	0.116006
13	0.125439
16	0.092841
21	0.081376

学習できたかどうかを判別するためにバックプロパゲーションの終了後、誤差伝搬をせず入力信号として正しい正弦波の波形を送ったときにどうなるかという実験を行った。図 6.4にその結果を示す。図 6.4の横軸は時間を表し、''・''はカオスニューロンの出力、点線は教師信号の出力である。これを見てみると、分割数が11, 13の時は点線から若干ずれているように見えるが、分割数16, 分割数21の時は点線に沿っている様に見える。また、この時の各分割数における誤差を表 6.1に示す。これらの結果より、誤差が0.1以下のときに学習成功と定義することにする。

**図 6.5:** 分割数31において、バックプロパゲーション終了後に、出力を入力に戻した時のカオスニューロンの動作
$\includegraphics[scale=1.0]{fig/sin/afterpro2/gnu1-31_after2.eps}$

**図 6.6:** 分割数37において、バックプロパゲーション終了後に、出力を入力に戻した時のカオスニューロンの動作
$\includegraphics[scale=1.0]{fig/sin/afterpro2/gnu1-37_after2.eps}$

時系列データを予測するには正しい信号が途絶えてもその次の未来を予測し続けなければならない。よって、バックプロパゲーションが終了してから、カオスニューロンの出力を入力に戻すことでその次の値の予測を行う。これを動作させた結果を図 6.5,図 6.6に示す。分割数が31の例では、次の値を予測し続けれているが、分割数が37の例においてはカオスニューロンの値が収束してしまい、値が一定となってしまった。もちろん誤差が大きい場合は収束するが、誤差が小さければ予測し続けれるといった特徴は見られなかった。また、分割数が極端に小さい値においては予測ができることが分かった。

**図 6.7:** 分割数20の正弦波を学習させた時の教師信号の出力
$\includegraphics[scale=1.0]{fig/sin/gnu1-20_inp.eps}$

**図 6.8:** 分割数20の正弦波を学習させた時のカオスニューロンの出力
$\includegraphics[scale=1.0]{fig/sin/gnu1-20_out.eps}$

次に学習に成功した場合のカオスニューロンの出力に着目する。代表例として、分割数が20における教師信号とカオスニューロンの出力のグラフを図 6.7, 図 6.8に表す。これらのグラフを比較してみると、カオスニューロンの出力は、望ましい出力（教師信号）の出力値よりも小さな値を示すことが分かった。

**図 6.9:** 分割数10の正弦波を学習させた時の最大誤差の変位
$\includegraphics[scale=1.0]{fig/sin/out_of_neuron_ck10.eps}$

**図 6.10:** 分割数19の正弦波を学習させた時の最大誤差の推移
$\includegraphics[scale=1.0]{fig/sin/out_of_neuron_ck19.eps}$

次に最大誤差の推移のグラフについて検討する。学習に成功した代表例として、分割数が10, 19の正弦波における最大誤差の推移のグラフを図 6.9, 図 6.10に表す。図 6.9では、誤差の変動にほとんどばらつきが見られない右肩下がりの曲線となった。図 6.10では、図 6.2と少し似ていて学習開始付近の時間では誤差に大きくばらつきはあるが、学習時間が200を過ぎた辺りから、そのばらつきと共に誤差が減少していくようなグラフとなっている。図 6.2, 図 6.9, 図 6.10を比べてみると、どれも学習の仕方に違いがあるように見れる。これについて後ほど検討することにする。また、各分割数におけるエリート遺伝子のパラメータを表 6.2に示す。

**表 6.2:** エリート遺伝子のパラメータ
	カオスニューロン			バックプロパゲーション
		$\alpha$			$\eta$
4	7.382812	0	0.5625	0.9375	0.25
10	2.226562	0.28125	0.625	0.6875	0.0625
19	6.523438	0.34375	0.3125	0.21875	0.15625

**図 6.11:** 分割数10におけるエリート遺伝子を分割数1から50の正弦波に適用した時の最大値
$\includegraphics[scale=1.0]{fig/sin/used_ck10s_elete_gene/elete_gclock_pt1.eps}$

次に、入力する波形のパターンを変えても同じパラメータで動作できるのかを調べる実験を行った。まず、分割数10の遺伝子を選択し、分割数1〜50の正弦波にそのパラメータを適用して学習を行った。その結果を図 6.11に示す。分割数10によって得られたエリート遺伝子と比べると、全体的に学習できていないことが分かる。

**図 6.12:** 分割数10のエリート遺伝子を分割数42の正弦波に適用した時の最大誤差の推移
$\includegraphics[scale=1.0]{fig/sin/used_ck10s_elete_gene/gnu1-42_gosa.eps}$

先ほどの実験で、それぞれの分割数によって、エリート遺伝子を適用した時のカオスニューロンの学習の仕方に違いがあることが分かった。この違いは適用した遺伝子にあるのではないのかと考え、分割数10の正弦波の学習によって得られたエリート遺伝子を分割数42の正弦波の学習に用いる実験を行う。この時のバックプロパゲーションにおける誤差の推移は図 6.12のようになった。このグラフを見てみると、図 6.9の特性と似たような学習の仕方をしていることが分かる。

これらの結果より、入力波形によってカオスニューラルネットやバックプロパゲーションのパラメータが適している値は異なり、同じ遺伝子を使って学習できるならば、似たような学習をするという傾向があることが分かる。

図 6.13: 各交叉方法における最終世代の遺伝子の評価値

$\includegraphics[scale=0.6]{fig/sin/kousa/ck4_old1.eps}$	$\includegraphics[scale=0.6]{fig/sin/kousa/ck4_old2.eps}$
()一点交叉+エリート保存選択の時	()二点交叉+一様交叉+エリート保存選択の時

今回用いた一点交叉は、ホランドが最初に提案したときの交叉方法であるが、効率は低く現在ではあまり使われていないことが文献[8]により分かったので、交叉方法として効率の良い２点交叉、一様交叉を用いることにした。図 6.13に最終世代の遺伝子の評価値を示す。このグラフの遺伝子番号41(右端)の遺伝子は、１つ前の世代のエリート遺伝子を引き継いだものでり、遺伝子番号が1〜40の遺伝子が一点交叉、もしくは２点交叉＋一様交叉である。これらを比較すると、２点交叉＋一様交叉の方が誤差の小さい値を多く示している。よって、以降の実験ではこの手法を用いることにする。