


: ニューラルネットワークの学習
: カオスニューラルネットワーク
: カオスニューロン
目次
カオスニューロン同士が相互結合をして構成されるニューラルネットワークを
カオスニューラルネットワークと呼ぶ。
カオスニューロンの入力はネットワーク外部から受けとるものと、
フィードバック入力に分けモデル化される。
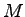 個の外部入力と
個の外部入力と 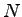 個のニューロン間の
相互結合を持つカオスニューラルネットワークの
個のニューロン間の
相互結合を持つカオスニューラルネットワークの 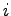 番目のニューロンの振舞いは、式(3.4)で表される。[5]
番目のニューロンの振舞いは、式(3.4)で表される。[5]
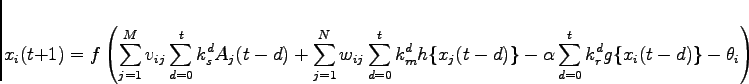 |
(7) |
式(3.4)で用いるそれぞれの変数が表す意味を以下に示す。
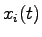 : 時刻
: 時刻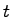 における
における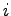 番目(
番目(
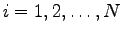 )のニューロンの出力
)のニューロンの出力
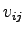 :
: 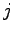 番目の外部入力
番目の外部入力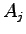 から
から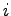 番目のニューロンへの重み
番目のニューロンへの重み
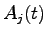 : 時刻
: 時刻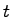 における
における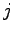 番目(
番目(
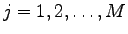 )の外部入力の大きさ
)の外部入力の大きさ
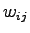 :
: 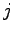 番目のニューロンから
番目のニューロンから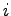 番目のニューロンへの重み
番目のニューロンへの重み
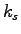 : 外部入力項に対する時間減衰定数(
: 外部入力項に対する時間減衰定数(
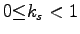 )
)
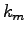 : 他のニューロンからのフィードバック入力項に対する時間減衰定数
: 他のニューロンからのフィードバック入力項に対する時間減衰定数
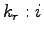 番目のニューロンの不応性の時間減衰定数(
番目のニューロンの不応性の時間減衰定数(
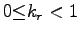 )
)
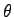 :しきい値
:しきい値
このとき、外部からの入力を表す項を 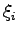 、
ニューロン間の相互結合を表す項を
、
ニューロン間の相互結合を表す項を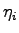 、
ニューロン自身の不応性の項を
、
ニューロン自身の不応性の項を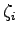 で表し、
で表し、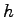 と
と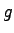 を恒等関数とすれば
次のように簡略化できる。
を恒等関数とすれば
次のように簡略化できる。
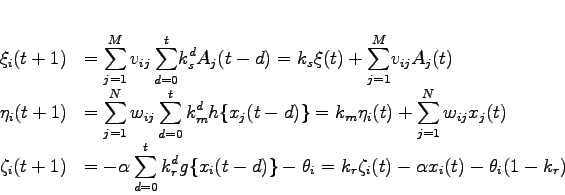 |
(8) |
式(3.5)を代入すると、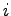 番目のニューロンの出力は次のように表される。
番目のニューロンの出力は次のように表される。
![\begin{displaymath}
x_i(t+1) = f[\xi_i(t+1)+\eta_i(t+1)+\zeta_i(t+1)]
\end{displaymath}](img69.png) |
(9) |
Deguchi Lab.
平成21年3月6日
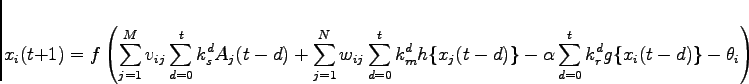
![]() 、
ニューロン間の相互結合を表す項を
、
ニューロン間の相互結合を表す項を![]() 、
ニューロン自身の不応性の項を
、
ニューロン自身の不応性の項を![]() で表し、
で表し、![]() と
と![]() を恒等関数とすれば
次のように簡略化できる。
を恒等関数とすれば
次のように簡略化できる。
![]() 番目のニューロンの出力は次のように表される。
番目のニューロンの出力は次のように表される。