合原らのヤリイカの巨大軸索を用いた実験[3]により、ニューロン内にもカオス現象が存在すること
が明らかにされた。前章で述べたような従来のニューロンモデルでは、多数の入力の結合荷重と
閾値作用をニューロンの特徴的な機能として採用し、モデル化を行ってきた。これは、実際の生物の神
経細胞には代謝や分裂といった様々な特徴が見られるが、忠実にニューロンをモデル化すると取り扱い
が複雑になり、その本質を理解するのに障害になると考えられていたからである。
従来のニューロンモデルの出力は、階段関数を用いた離散的なものだと考えられていたが、実際の神経
細胞に対して空間固定の条件で注意深い実験を行うと、神経膜の活動電位生成過程は厳密には階段関
数には従わず、急峻ではあるが連続的に応答の大きさが変化していることがわかった。
合原らは、従来のニューロンモデルの出力関数を連続関数に変更したカオスニューロンモデルを提案
している。これは式(3.1)で表される。
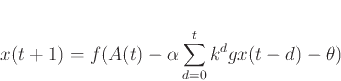 |
(2) |
ここで、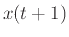 は時刻
は時刻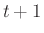 におけるニューロンの出力、
におけるニューロンの出力、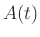 は時刻
は時刻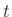 における外部入力の大きさ、
における外部入力の大きさ、
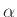 は不応性の項に対するスケーリングファクタ(
は不応性の項に対するスケーリングファクタ(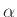
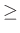 0)、
0)、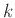 は不応性の定数
(0
は不応性の定数
(0 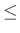 k
k 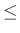 1)、
1)、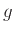 は軸索の伝達関数である。不応性とはニューロンが興奮した後、一時的に閾
値が上昇する性質のことである。また、膜電位や不応性は減衰されながらもしばらくの間残る。
関数fはニューロンの内部状態と出力の関係を表し、合原らのモデルではFigure 3.1で表せ
られるシグモイド関数が用いられている。その式は、式(3.2)で表される。[2]
は軸索の伝達関数である。不応性とはニューロンが興奮した後、一時的に閾
値が上昇する性質のことである。また、膜電位や不応性は減衰されながらもしばらくの間残る。
関数fはニューロンの内部状態と出力の関係を表し、合原らのモデルではFigure 3.1で表せ
られるシグモイド関数が用いられている。その式は、式(3.2)で表される。[2]
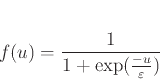 |
(3) |
Deguchi Lab.
2017年3月6日