ベクトル空間法[11]

前節ではある文書における各単語の重要度を算出した。 次にその重要度を利用して、ベクトル空間法という計算方法を用い、複数の文書同士の類似度を計算する。

ベクトル空間法とは、文書を多次元空間上のベクトルとして表現し、 二つのベクトルを比較することにより類似度を調べるものである。 つまり、ベクトルの方向は文書の特徴であるので、二つのベクトルのなす角が小さいほど似ているということである。

$m$ 個のタームを持つ文書$D$ を形態素解析し、各ターム毎の重要度を $w_{D1}, w_{D2}, \ldots , w_{Dm}$ としたとき、 文書$D$ のベクトルは以下のように表される。

$$\vec{D}=\left( w_{D1}, w_{D2}, \ldots , w_{Dm}\right)$$ (3.16)

今、$n$ 個のタームを持つ文書$E$ が文書$D$ と どの程度類似しているのかということを考えたとき、 文書$E$ も式(3.16)から同様に $\vec{E}=\left(w_{E1}, w_{E2}, \ldots , w_{En}\right)$ となる。

これらベクトル $\vec{D}$ とベクトル $\vec{E}$ の類似度の計算は以下の式で実現できる。

$$sim(\vec{D},\vec{E})=\cos \theta = \frac{\vec{D} \cdot \vec{E}}{\vert\vec{D}\vert\vert\vec{E}\vert}$$ (3.17)

ここで、$\theta$ はベクトル$\vec{D}$ とベクトル$\vec{E}$ のなす角であり、 $sim(\vec{D},\vec{E})$ は、文書Dと文書Eの類似度である。

以下の例文で実際に類似度の計算を行う。

例１

Ｃ言語のプログラムを理解できる．

Ｃ言語の簡単なプログラムを作成できる．

有用なアルゴリズムを理解する．

例２

Ｃ言語の簡単なプログラムを作成できる．

アルゴリズム（サーチ，ソートなど）を理解できる．

次に、この例1、例2を形態素解析し、重要度を計算したものを表3.1に示す。

表 3.1: 例文1、例文2の重要語およびその重要度

用語	例文1	例文2
C言語	3.46	1.41
プログラム	2.00	1.00
アルゴリズム	1.00	1.00
サーチ		1.00
ソート		1.00

この例1、例2は式(3.16)の形式に表すと

$$\vec{D}_{\mbox{例1}} = ( 3.46 , 2.00 , 1.00 )$$

$$\vec{D}_{\mbox{例2}} = ( 1.41 , 1.00 , 1.00 , 1.00 , 1.00)$$

となる。重要度はそれぞれ、左の要素から( C言語 , プログラム , アルゴリズム , サーチ , ソート )と対応している。

次に、この2つのベクトルの大きさを計算する。

$$\vert\vec{D}_{\mbox{例1}}\vert = \sqrt{ 3.46^2 + 2.00^2 + 1.00^2 }$$

$$= 4.12$$

$$\vert\vec{D}_{\mbox{例2}}\vert = \sqrt{ 1.41^2 + 1.00^2 + 1.00^2 + 1.00^2 + 1.00^2}$$

$$= 2.45$$

最後に式(3.17)より、この2つの例文の類似度を計算する。

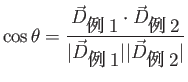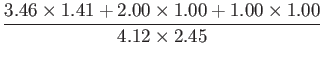$$sim(\vec{D}_{\mbox{例1}},\vec{D}_{\mbox{例2}}) = \cos \theta = \frac{\vec{D}_{\mbox{例1}} \cdot \vec{D}_{\mbox{例2}}}{\vert\vec{D}_{\mbox{例1}}\vert\vert\vec{D}_{\mbox{例2}}\vert}$$

$$= \frac{3.46 \times 1.41 + 2.00 \times 1.00 + 1.00 \times 1.00}{4.12 \times 2.45}$$

$$= 0.78$$

よって、例1、例2の類似度は0.78であることがわかる。