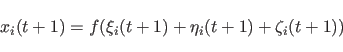 |
(2.4) |
合原らのヤリイカの巨大軸索を用いた実験により、 ニューロン内にもカオス現象が存在することが明らかにされた[4]。 従来のニューロンモデルでは、多数の入力の結合荷重としきい値作用をニューロンの特徴的な機能として採用し、モデル化を行なってきた。 これは、 忠実にニューロンをモデル化すると取り扱いを複雑にし、その本質を理解するのに障害になると考えられていたからである。 さらに出力関数に関しても階段関数で表されている。
しかし合原らの実験によると、実際のニューロンは2.2節で述べたようなニューロンモデルとは違い、発火後に閾値が一時的に高くなり発火し難くなる性質である不応性を持つことと、ニューロンの応答が離散的ではなく連続的であるということが明らかにされた。
そこで合原らにより、これらの特徴を取り入れたカオスニューロンが考案された。 カオスニューラルネットワークとはカオスニューロンで構成されたネットワークである。 ニューロンとカオスニューロンの違いとして不応性を持つ点と入力の時間的加算がある点があげられる[5]。 カオスニューロンの入力はネットワーク外部から受けとるものと、他のニューロンの出力とに分けモデル化される。 以下にカオスニューロンの式を示す。
ここで![]() は時刻
は時刻![]() での
での![]() 番目のニューロンの出力を表す。出力関数
番目のニューロンの出力を表す。出力関数![]() は図 2.6のシグモイド関数を用いる。この関数は式 (2.5)で表される。
は図 2.6のシグモイド関数を用いる。この関数は式 (2.5)で表される。![]() はシグモイド関数の立ち上がりの鋭さを表す。
従来のニューロンモデルの出力は、全か無かの法則で与えられていたが実際の神経細胞において実験を行うと厳密には全か無かの法則には従わずシグモイド関数のように、急峻ではあるが連続的に応答の大きさが変化する事が分かっている。
なので、単体でカオスを生成するため実際の神経細胞に合わせ、カオスニューロンではシグモイド関数が使用されている。
はシグモイド関数の立ち上がりの鋭さを表す。
従来のニューロンモデルの出力は、全か無かの法則で与えられていたが実際の神経細胞において実験を行うと厳密には全か無かの法則には従わずシグモイド関数のように、急峻ではあるが連続的に応答の大きさが変化する事が分かっている。
なので、単体でカオスを生成するため実際の神経細胞に合わせ、カオスニューロンではシグモイド関数が使用されている。
また、シグモイド関数![]() の入力として、外部からの入力に関する項
の入力として、外部からの入力に関する項![]() 、
他のニューロンからの入力に関する項
、
他のニューロンからの入力に関する項![]() 、不応性に関する項
、不応性に関する項
![]() とに分けられ、
それぞれ以下の式で定義される[6]。
とに分けられ、
それぞれ以下の式で定義される[6]。
以下にそれぞれの変数が表す意味を示す。