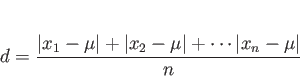


Next: 尖度
Up: 統計量
Previous: 統計量
目次
いくつかのデータがあるとき、その平均は同じでも分布の様子が異なっている場合がある。
データの広がりを表す数値を散布度という。
最も簡単な散布度は、最大値と最小値の差である。
これを範囲(レンジ)といい、Rで表す。
範囲は簡単に求められるという利点を持つが最大値と最小値のみに依存するため、
それ以外のデータのちりばり具合を表していない。
そこで、それ以外のすべてのデータを用いた散布度を定義する。
それにはデータの平均に着目して、データ全体として平均からどの程度広がっているか見ればよい。
いま、変量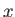 のデータを
のデータを 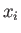 (
(
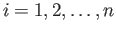 )とするとき、
各々のデータ
)とするとき、
各々のデータ 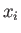 と平均
と平均 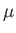 との隔たり(これを偏差という)は
との隔たり(これを偏差という)は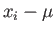 で表される。
散布度の定義として、まず偏差の絶対値の平均
で表される。
散布度の定義として、まず偏差の絶対値の平均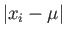 の平均
の平均
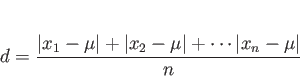 |
(5.3) |
が考えられる。この散布度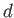 を平均偏差という。しかし、絶対値は一般に取り扱いにくいため、偏差を2乗したものの平均
を平均偏差という。しかし、絶対値は一般に取り扱いにくいため、偏差を2乗したものの平均
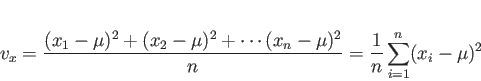 |
(5.4) |
によって散布度を定めることにする。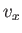 をデータの分散という。また、分散
をデータの分散という。また、分散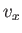 の正の平方根をとったものをデータの標準偏差といい。
の正の平方根をとったものをデータの標準偏差といい。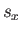 で表す。
で表す。
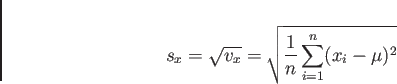 |
(5.5) |
Deguchi Lab.
2013年2月28日