![\includegraphics[scale=1.2]{eps1/neuron_model.eps}](img5.png)
|
この図の![]() は対象となるニューロンの
は対象となるニューロンの![]() 番目の入力であり、0または1のパルス入力である。
番目の入力であり、0または1のパルス入力である。
![]() は結合荷重と呼ばれ、シナプス結合の強さを示す。
は結合荷重と呼ばれ、シナプス結合の強さを示す。
![]() はニューロンに対する閾値であり、ニューロンの電位がこれを超えるとニューロンは発火する。
また、
はニューロンに対する閾値であり、ニューロンの電位がこれを超えるとニューロンは発火する。
また、![]() は出力である。
このニューロンモデルの作用は以下の式で表すことが出来る。
は出力である。
このニューロンモデルの作用は以下の式で表すことが出来る。
式(2.1)で、![]() を膜電位又は内部ポテンシャルと呼ぶ。
この式は、ニューロンが
を膜電位又は内部ポテンシャルと呼ぶ。
この式は、ニューロンが![]() 番目の入力を受けて
番目の入力を受けて![]() になると、ニューロンの膜電位が
になると、ニューロンの膜電位が![]() 高くなることを表す。
この時、
高くなることを表す。
この時、![]() ならばそのシナプス結合は興奮性、
ならばそのシナプス結合は興奮性、![]() ならば抑制性、また、
ならば抑制性、また、![]() ならばシナプス結合は成されていないことになる。
ならばシナプス結合は成されていないことになる。
![]() は閾値であり、各入力にシナプスの重みを掛けた荷重和
は閾値であり、各入力にシナプスの重みを掛けた荷重和
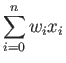 がこの値を超えた時に
がこの値を超えた時に![]() の値は正となり、ニューロンが興奮する。
このモデルでは、入力と出力は共に0と1の離散的な値である。
式(2.2)の出力関数は以下のように与えられている。
の値は正となり、ニューロンが興奮する。
このモデルでは、入力と出力は共に0と1の離散的な値である。
式(2.2)の出力関数は以下のように与えられている。
この関数は階段関数であり、図2.3のようになる。
マッカロとピッツのモデルは離散的な入出力であるが、連続的なモデルを考える場合はシグモイド関数と呼ばれるものを出力関数とすることが多い。 シグモイド関数として有名なものに式(2.4)がある。
このシグモイド関数の特性は図2.4となる。