ヤングの式の証明。

岐阜高専　所　哲郎

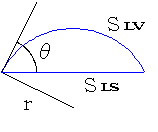
図の様な水滴を考える。水滴の表面はＳLVで、固体との接触面積はＳLSとする。接触角はθ、体積はＶである。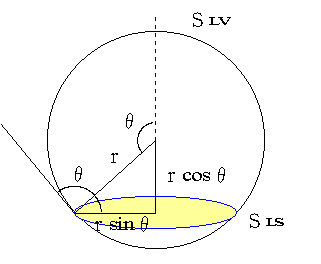

まず、ＳLV、ＳLS、Ｖを求めると、


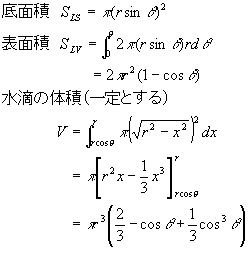
となる。ここで、水滴の体積を一定と考えれば、


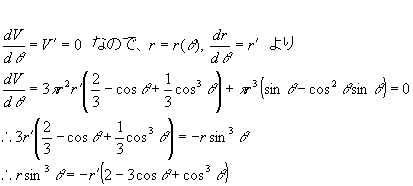
となる。

ここで、水滴系の全表面エネルギーを考えると、水滴の全表面エネルギーからの付着仕事による安定（エネルギーの減少）を考えれば良いので、


となる。この水滴が平衡状態にあるとすると、


である。上式をで割って、


となる。この式はであれば、　という、ヤングの式に一致する。なお、上記の証明は下記の通りである。

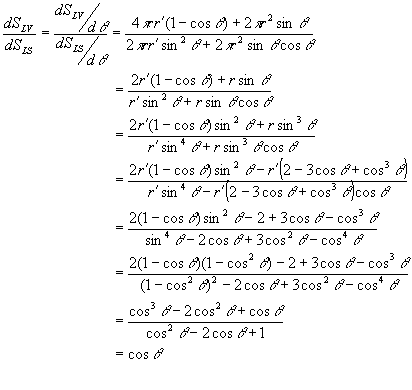
岐阜工業高等専門学校　電気工学科　所研究室

http://www.gifu-nct.ac.jp/elec/tokoro/