数値計算法　常微分方程式

<<オイラー法>>

オイラー法により， つぎのバネ-ダンパ系の微分方程式を解くプログラム．

M*(d^2x/dt^2)+p*(dx/dt)+q*x=A*sin(ωt)

ただし，

t : 時間(s)，x : 振幅(m) M : 質量(kg)，p : ダンパの係数(kg/s)，q : バネ係数(kg/s^2)

A : 外力の大きさ(kgm/s^2)，ω : 外力の振動数(rad/s)

<仕様>
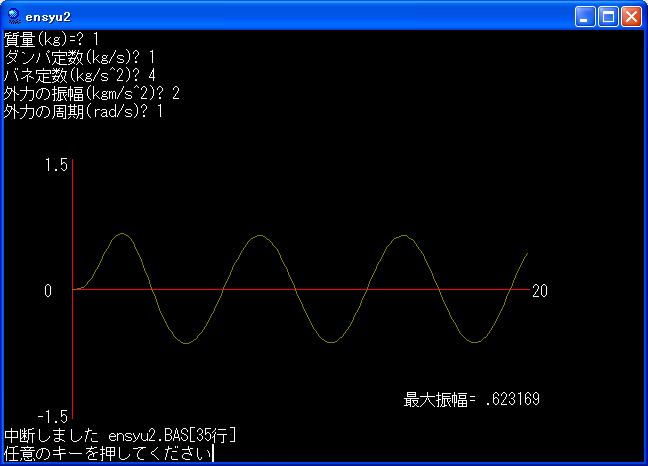
・入力はM，p，q，A，ω
・初期条件はx=0, dx/dt=0とする．
・時間の刻み幅は0.1(s)とし，0秒から20秒まで計算する．
・出力は10秒から20秒の間までの振幅で最大のもの（最大振幅）

使用言語　F-BASIC

' オイラー法により微分方程式を解く．
' バネ-ダンパ系の強制振動運動方程式
window(-3,-3)-(25,2)
'
declare function FX(X)
declare function FY(X,Y,T)
'
X=0		'位置の初期条件
Y=0		'速度(dx/dt)の初期条件
MAX=0		'最大振幅の初期設定
DT=0.1		'時間の刻み幅
'
input "質量(kg)=";M
input "ダンパ定数(kg/s)";P
input "バネ定数(kg/s^2)";Q
input "外力の振幅(kgm/s^2)";A
input "外力の周期(rad/s)";OMEGA
'
'グラフィックの初期化
line (0,-1.5)-(0,1.5),pset,5
line (0,0)-(20,0),pset,5
locate  4,14 : print 0
locate  4, 7 : print 1.5
locate  4,21 : print -1.5
locate 65,14 : print 20
point(X,0)
'オイラー法
for T=0 to 20 step DT
   X=X+FX(Y)*DT
   Y=Y+FY(X,Y,T)*DT
   line -(T,-X),pset,12
   if T>=10 and MAX< abs(x) then MAX=abs(X)
next T
locate 50,20 : print "最大振幅=";MAX
stop
end
'
function FX(Y)
  FX=Y
end function
'
function FY(X,Y,T)
  shared M,P,Q,A,OMEGA
  FY=(A*sin(OMEGA*T)-P*Y-Q*X)/M
end function

図１　実行結果

数値計算法に戻る