


: 安定性
: sysconh16
: 最小実現
前節で最小実現の性質について幾つか説明した.本節では伝達関数行列が与えられたとき,その最小実現を具体的に求めるためのアルゴリズムについて説明する.
最小実現のアルゴリズムⅠ(Mooreの方法)
- 与えられた伝達関数を次の形に変形する.
ただし分母の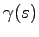 は,
は,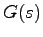 の各要素の分母の最小公倍多項式であり,
の各要素の分母の最小公倍多項式であり,
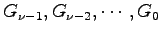 は
は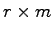 の定数行列である.
の定数行列である.
を求める.(容易に確かめられる?ようにシステム
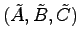 は一つの可制御な
は一つの可制御な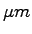 次元の実現である.)
次元の実現である.)
- 2.の
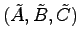 が可観測ならば最小実現,そうでなけれはシステム
が可観測ならば最小実現,そうでなけれはシステム
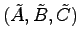 を正準分解して,可制御可観測なサブシステム
を正準分解して,可制御可観測なサブシステム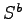 を求める.システム
を求める.システム
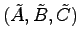 には不可制御なサブシステム
には不可制御なサブシステム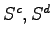 は存在しない.したがってまず
は存在しない.したがってまず
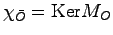 の任意の基底を
の任意の基底を
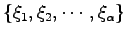 とし,ついで
とし,ついで
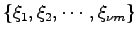 が
が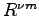 の基底となるように独立なベクトル
の基底となるように独立なベクトル
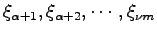 を選び,
を選び,
![$T^{-1}= [ \xi_1, \xi_2, \cdots, \xi_{\nu m}]$](img708.png) とおくと,教科書3.4節の結果より
とおくと,教科書3.4節の結果より
を得る.さらに
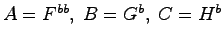 とおくとシステム
とおくとシステム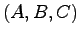 が一つの最小実現である.
が一つの最小実現である.
例4.3 伝達関数行列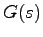 が
が
で与えられるとき,これの最小実現を求める.
上記のアルゴリズムⅠにしたがって計算すると,
-
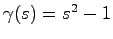 であるから
であるから
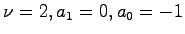 となる.また例4.2より
となる.また例4.2より
である.
-
- システム
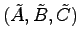 を正準分解する.ただし,前述のアルゴリズムⅠの記述にもあるように,システムは可制御であるから,可観測性について分解すればよい.したがって可観測性行列
を正準分解する.ただし,前述のアルゴリズムⅠの記述にもあるように,システムは可制御であるから,可観測性について分解すればよい.したがって可観測性行列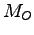 を求めると
を求めると
であるから,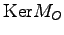 の基底を求めるため
の基底を求めるため
を計算すると
となり,結局
となる.したがって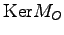 の基底として
の基底として
![$\xi_1 = \left[ \begin{array}{cccc}
1 & 0 & 1 & 0 \end{array}\right]^T$](img718.png) ととることができる.残りを適当に選べば
ととることができる.残りを適当に選べば
等とすることができる.これにより
となる.よって
が一つの最小実現となる.
最小実現のアルゴリズムⅠ' アルゴリズムⅠに双対なアルゴリズムとして,アルゴリズムⅠの手順2において次のシステム係数を取ることが考えられる.
このときシステム
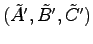 は,可観測な
は,可観測な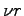 次元の実現となるが,これを正準分解して,可制御可観測なサブシステムを求めればよい.
次元の実現となるが,これを正準分解して,可制御可観測なサブシステムを求めればよい.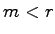 であればアルゴリズムⅠを利用し,
であればアルゴリズムⅠを利用し,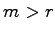 であればアルゴリズムⅠ’を利用すれば,扱うシステムの次元数が小さくなるので計算が容易である.
であればアルゴリズムⅠ’を利用すれば,扱うシステムの次元数が小さくなるので計算が容易である.
つぎに限定的ではあるが,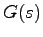 の各要素の極がすべて実数の単極の場合に適用可能な,最小実現を直接求めるためのアルゴリズムを示す.
の各要素の極がすべて実数の単極の場合に適用可能な,最小実現を直接求めるためのアルゴリズムを示す.
最小実現のアルゴリズムⅡ
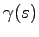 の根
の根
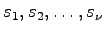 を求める.
を求める.
-
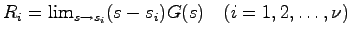 を求める.
を求める.
-
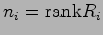 および
および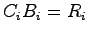 となる
となる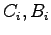 を求める.ただし
を求める.ただし
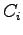 及び
及び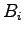 は
は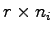 及び
及び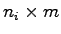 の行列である.
の行列である.
- システムの係数行列を
とする.
例4.4 例4.3の最小実現をアルゴリズムⅡにより求める.
伝達関数行列は
であるから
-
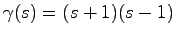 より,明らかに
より,明らかに
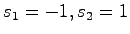 である.
である.
-
-
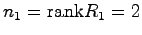 ,
,
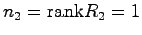 である.これより
である.これより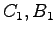 を
を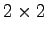 行列で,
行列で,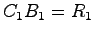 を満たすように選ぶ.例えば,単位行列を利用して
を満たすように選ぶ.例えば,単位行列を利用して
とすることができる.また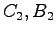 は
は
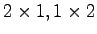 行列で
行列で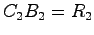 を満たせばよい.これについては,例えば
を満たせばよい.これについては,例えば
と選べばよい.
-
となる.



: 安定性
: sysconh16
: 最小実現
endo
平成16年6月30日
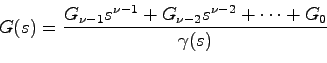
![\begin{eqnarray*}
\tilde{A} &=& \left[ \begin{array}{c\vert c}
0 & I_{(\nu-1)m} ...
...n{array}{cccc} G_0 & G_1 & \cdots & C_{\nu-1}
\end{array}\right]
\end{eqnarray*}](img701.png)
![\begin{displaymath}
F = T\tilde{A}T^{-1} = \left[ \begin{array}{cc}
F^{aa} & F^{...
...{C}T^{-1} = \left[ \begin{array}{cc}0 & H^b \end{array}\right]
\end{displaymath}](img709.png)
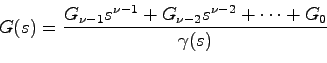
![\begin{eqnarray*}
\tilde{A} &=& \left[ \begin{array}{c\vert c}
0 & I_{(\nu-1)m} ...
...n{array}{cccc} G_0 & G_1 & \cdots & C_{\nu-1}
\end{array}\right]
\end{eqnarray*}](img701.png)
![\begin{displaymath}
F = T\tilde{A}T^{-1} = \left[ \begin{array}{cc}
F^{aa} & F^{...
...{C}T^{-1} = \left[ \begin{array}{cc}0 & H^b \end{array}\right]
\end{displaymath}](img709.png)
![]() が
が
![\begin{displaymath}
G(s) = \left[ \begin{array}{cc}
\displaystyle{\frac{2}{s+1}}...
...rac{1}{s+1}} & \displaystyle{\frac{1}{s+1}}
\end{array}\right]
\end{displaymath}](img692.png)
![\begin{displaymath}
G_1 = \left[ \begin{array}{cc}
2 & 0 1 & 1 \end{array}\ri...
... \left[ \begin{array}{cc}
-2 & 2 -1 & -1 \end{array}\right]
\end{displaymath}](img712.png)
![\begin{displaymath}
\tilde{A} = \left[ \begin{array}{cc\vert cc}
0 & 0 & 1 & 0 \...
...ay}{cccc}
-2 & 2 & 2 & 0 -1 & -1 & 1 & 1 \end{array}\right]
\end{displaymath}](img713.png)
![\begin{displaymath}
M_O = \left[ \begin{array}{cccc}
-2 & 2 & 2 & 0 \\
-1 & -1 ...
... & 1 \\
2 & 0 & -2 & 2 \\
1 & 1 & -1 & -1
\end{array}\right]
\end{displaymath}](img714.png)
![\begin{displaymath}
M_O \left[ \begin{array}{c}x_1 x_2 x_3 x_4 \end{array}\right] = 0
\end{displaymath}](img715.png)
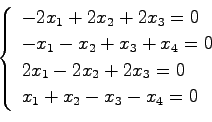
![$\xi_1 = \left[ \begin{array}{cccc}
1 & 0 & 1 & 0 \end{array}\right]^T$](img718.png) ととることができる.残りを適当に選べば
ととることができる.残りを適当に選べば
![\begin{displaymath}
T^{-1} = \left[ \begin{array}{cccc}
1 & 0 & -1 & 0 \\
0 & 1 & 0 & 0 \\
1 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \end{array}\right]
\end{displaymath}](img719.png)
![\begin{displaymath}
F = \left[ \begin{array}{c\vert ccc}
1 & 0 & 0 & 0 \hline...
...c\vert ccc}
0 & 2 & 4 & 0 0 & -1 & 2 & 1
\end{array}\right]
\end{displaymath}](img720.png)
![\begin{displaymath}
\dot{x} = \left[ \begin{array}{ccc}
0 & 0 & 1 0 & -1 & 0 ...
...\begin{array}{ccc} 2 & 4 & 0 -1 & 2 & 1 \end{array}\right]x
\end{displaymath}](img721.png)
![\begin{displaymath}
\tilde{A}' = \left[ \begin{array}{c\vert c}
0 & -a_0 I_r ...
...}' = \left[ \begin{array}{c\vert c}
0 & I_r \end{array}\right]
\end{displaymath}](img722.png)
![]() の各要素の極がすべて実数の単極の場合に適用可能な,最小実現を直接求めるためのアルゴリズムを示す.
の各要素の極がすべて実数の単極の場合に適用可能な,最小実現を直接求めるためのアルゴリズムを示す.
![\begin{displaymath}
A = \left[ \begin{array}{cccc}
s_1 I_{n_1} & & & 0 \\
& s_2...
...gin{array}{cccc} C_1 & C_2 & \cdots & C_\nu \end{array}\right]
\end{displaymath}](img736.png)
![\begin{displaymath}
G(s) = \left[ \begin{array}{cc}
\displaystyle{\frac{2}{s+1}}...
...rac{1}{s+1}} & \displaystyle{\frac{1}{s+1}}
\end{array}\right]
\end{displaymath}](img692.png)
![\begin{eqnarray*}
R_1 &=& \lim_{s \to -1}(s+1)G(s) =
\left[ \begin{array}{cc}
2 ...
...(s) =
\left[ \begin{array}{cc}
0 & 1 0 & 0 \end{array}\right]
\end{eqnarray*}](img739.png)
![\begin{displaymath}
C_1 = \left[ \begin{array}{cc}1 & 0 0 & 1 \end{array}\rig...
...) = \left[ \begin{array}{cc}2 & -1 1 & 1 \end{array}\right]
\end{displaymath}](img745.png)
![\begin{displaymath}
C_2 = \left[ \begin{array}{c} 1 0 \end{array}\right], \quad
B_2 = \left[ \begin{array}{cc} 0 & 1 \end{array}\right]
\end{displaymath}](img749.png)
![\begin{eqnarray*}
A &=& \left[ \begin{array}{cccc}
s_1 I_{n_1} & & & 0 \\
& s_2...
...eft[ \begin{array}{ccc}1 & 0 & 1 0 & 1 & 0 \end{array}\right]
\end{eqnarray*}](img750.png)