分析の手順

それぞれのサンプルに対して$p$ 個の変数をもつデータ $\myvec {x}_i (i=1,\cdots,n)$ があるとする。 いまサンプルの変数名を $x_{ij} (j=1,\cdots,p)$ とする。

$$\myvec {x}_i = [ \begin{array}{@{ }cccc@{ }} x_{i1} & x_{i2} & \cdots & x_{ip} \end{array} ] (i=1,\cdots,n)$$ (2.12)

各変数が結果に及ぼす影響を等しくするために、標準化変数 $\myvec {u}_i = [u_{ij}](j=1,\cdots,p)$ を考える。 ここで$j$ 番目の変数の平均値を $\overline{x_j} = \sum^{n}_{k=1}{x_{kj}/n}$ 、標準偏差を $s_j$ とすると次式を得る。

$$\myvec {u}_i = [ \begin{array}{@{ }cccc@{ }} u_{i1} & u_{i2} & \cdots & u_{ip} \end{array} ]$$ (2.13)

$$u_{ij} = \frac{x_{ij} - \overline{x_j}}{s_j} (i=1,\cdots,n,j=1,\cdots,p)$$ (2.14)

式(2.14)により各標準化変数は平均が0、分散が1に規格化されている。 $i$ 番目のサンプルの第１主成分の値（主成分得点）をつぎのようにおく。

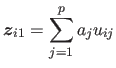$$\myvec {z}_{i1} = \sum^{p}_{j=1} a_{j} u_{ij}$$ (2.15)

すべての変数によるデータのばらつきを第１主成分に反映させるためには、分散 $V_{z1}$ が最大になる係数 $a_{j}(j=1,\cdots,p)$ を求めればよい。 式(2.14)において $u_{ij}$ の平均が0であることから $z_{i1}$ の平均も0となっている。 したがって、 $z_{i1}$ の分散を求める式は次式のように記述することができる。

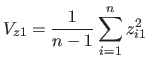$$V_{z1} = \frac{1}{n-1} \sum^{n}_{i=1} z^2_{i1}$$ (2.16)

上式より分散を最大にする係数は、つぎの相関係数行列の第1固有値（最大固有値） $\lambda _1$ に対応する大きさ1の固有ベクトル $\myvec {a} = [\begin{array}{@{ }ccc@{ }} a_1 & \cdots & a_p \end{array}]^t$ であり、$V_{z1}$ の最大値は $\lambda _1$ である。

$$\myvec {R} = \left[ \begin{array}{cccc} 1 & r_{x_1 x_2} & \cdot... ...ddots & \vdots \\ r_{x_p x_1} & r_{x_p x_2} & \cdots & 1 \end{array} \right]$$ (2.17)

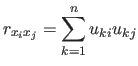$$r_{x_i x_j} = \sum^n_{k=1} u_{ki} u_{kj}$$ (2.18)

この実対称係数行列の固有値や固有ベクトルは、ヤコビ法や累乗法を用いて求めることができる。 第2主成分以降についても同様の手法で主成分得点を計算していくことができる。 第$k$ 主成分は係数行列$R$ の第$k$ 固有値に対応する大きさ1の固有ベクトルである。