カオスニューロン

  実際のニューロンでは容易にカオスが観察されるが、 2.2節に示したマカロックとピッツのニューロンモデルではカオスは観察されない。これは、マカロック・ピッツモデルでは考慮しなかった、実際のニューロンの有する機能・性質がカオスを生成しているためである。

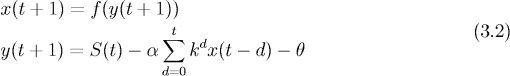
マカロック・ピッツモデルでは考慮しなかった実際のニューロンの有する機能・性質として、不応性が挙げられる。不応性とは 2.1節に記したように、ニューロンが発火した後、閾値が一時的に高くなり発火し難くなる性質のことである。高くなった閾値は時間の経過に伴い指数関数的に減衰する。

また、 2.1節の中でニューロンは全か無の法則に従う、つまり、ニューロンは図 2.2のように離散的な応答を示すとしたが、厳密には全か無の法則には従わず、応答の大きさは連続的である。

式(3.2)が、如上2点を機能・性質として新たに取り入れた、カオスの観察され得るニューロンモデルである。以降これをカオスニューロンと呼ぶ。

 

x(t)は時刻tでの出力、y(t)は時刻tでの内部状態、S(t)は時刻tでの入力、 は不応性の項に対する係数、kは不応性の時間減衰定数、 は閾値、f(y)は出力関数をそれぞれ表す。f(y)はシグモイド関数（式(3.3)、図 3.5）を用いる。

 

  
図 3.5: シグモイド関数( = 1)

はシグモイド関数の傾きの緩急を表す定数であり、小さいほどその傾きは急峻となる。

入力S(t)を時刻tによらず一定であるとし、

とおくと、式(3.2)は以下の式(3.5)に変形される。

 

を0から0.25まで変化させてy(10000)からy(12000)までの値を計算し、プロットしたグラフが図 3.6である。（ 、k = 0.5、a = 0.3とした。）

  
図 3.6: カオスニューロンの応答

カオスニューロンが図 3.1のロジスティック写像と似た応答を示すことがわかる。