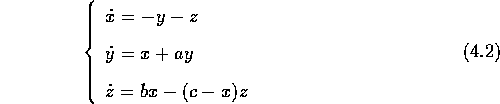
この節では、 本研究での学習の対象になるカオスアトラクタについての説明をする。 アトラクタ(attractor)は、 非線形力学システムにおいて過渡状態を経た後に定常的に観察される状態である。 2次元の相空間では、 アトラクタは点か閉曲線のどちらかでしか存在し得ないので、 次元はそれぞれ0次元、1次元となる。 ここで点の方は一般に平衡点、 閉曲線は周期起動であるため周期アトラクタと呼ばれる。
ところが相空間の次元が高くなるとアトラクタは複雑なものとなる。 3次元の相空間ではさらに準周期的な挙動を示す準周期アトラクタとカオスアトラクタが存在する。 カオスアトラクタについては次の例を見ながら説明する。
式(4.2)は西独の科学者レスラーが導き出した方程式であり、 科学反応中の振動や対流を表す方程式を簡単にしたものである。 散逸系であり、 解は図4.4のように3次元の相空間内の軌跡として表すことができる。 ただし、この時の初期値、 パラメータはそれぞれ (a,b,c)=(0.344,0.4,4.5) 、 (x,y,z)=(1.0,0.0,0,0)) である。
この相空間は次のプロセスを不規則に繰り返しながら、 非周期的で複雑な挙動を示す。
この奇妙な軌道は、 初期値を変えても現れるためアトラクタであるということが分かる。 これがカオスアトラクタである。 前にも述べたが、 このようなカオスアトラクタは初期値に鋭敏に反応するため、 近い位置に二つの初期値を設定してもそれらは全く別の軌道を描いていく。 さらに、 これがカオスアトラクタであるという理由の一つとして軌道の予測が不可能であるという点がある。 ある時刻に軌道がどこにあるのかというのは正確には分からないため、
少しでも予測が違うと、 初期値鋭敏性によりまた遠く離れていってしまうのである。
本研究の目的は、 ニューラルネットワークにこのカオスアトラクタを学習させることであるが、 実際には3次元のアトラクタそのものを学習させるわけではなく、 そのダイナミクスを学習させることになる。 また微分方程式のアトラクタは、 アトラクタと交わった平面である図4.5のような断面により、 差分方程式に変換することができるので、 本研究では差分方程式のダイナミクスをネットワークに学習させることにする。