「直交したパターンは成功しにくい」ことはわかっているが，4 パターンあたりの 直交数により，どの程度想起に成功するかを調べる必要がある。 ここでは，この直交数を変えて調査を行なう。
そこで，直交の数が 1 から 6 までの 6 通りについて 
のパターンを
作成し，同じように検索を行なった。
まず，直交数を区別せずに，すべてを一緒にまとめると， 図 7.7, 7.8 の「全範囲」となる。 内積値が小さいほど，成功率が悪くなっている。 また，この場合も，直交を含まない場合と同じように 12 を境に成功率が大きく 変わっているので， 内積値が 12 以下を「直交に近いパターン」と考えた方が良いことがわかる。
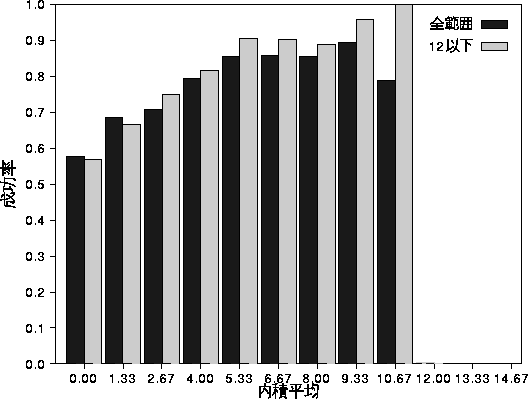
図 7.7: 相関内積と想起成功率の関係（直交あり，1 パターン 3 通り）
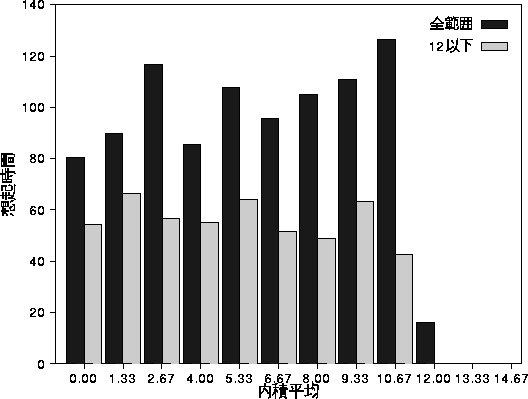
図 7.8: 相関内積と想起時間の関係（直交あり，1 パターン 3 通り）
また，同じように内積平均が 12 以下のみでまとめると，この 図 7.7, 7.8 の「12 以下」のようになる。 この場合，内積平均 8 前後の成功率が高くなっている。 しかし，4 より小さくなるにしたがって，範囲の限定の有無に関わらず， 成功率が悪くなっている。 よって，確かに直交に近くなるにしたがって，想起しにくくなることがわかる。 しかし，内積値が大きい時のように全く想起されないということはない。 また，想起時間も短縮されているが，成功した場合は内積平均に関わらず， ほぼ一定の時間で想起している。つまり， 内積値の大きいものを含むパターンのように，長時間かかることがない。
次に，前節で調べた直交を含まないパターン（直交数 0）も合わせて， 直交数と成功率，想起時間の関係についてまとめると， 図 7.9, 7.10 のようになる。 この場合も「全範囲」と「12 以下」を比較した。
「全範囲」では， 成功率は 0.6 前後で，時間はかえって直交数が少ない方がかかることになる。 「12 以下」でまとめると，直交数が少ないほど成功率が高くなるが， 成功した時の想起時間は，直交数に関わらずほぼ一定となっている。
以上の結果から，直交が含まれていても直交数が少なければ，成功率が高くなる。 つまり，「成功率が悪い直交したパターン」とは，直交数が 5, 6 のような多いもの であるといえる。 また，直交しているパターンが多くても，成功率を高めれば， 短時間で想起できる理想的なパターンになると考えられる。 なお，この改良は，第 8 章で行なう。
次節では，直交数と内積平均をさらに限定し，成功しやすいパターンを求める。
