高木・菅野のファジィ推論は後件部にファジィ集合ではなく線形(非線形)式を用いたファジィ推論法です。事実として入力される値をx1゜、x2゜とすると、高木・菅野のファジィ推論は以下に示す形態で表されます。
ルール1:If x1 is A11 and x2 is A12 , then y = a11(x1゜) + a12(x2゜) + b1
ルール2:If x1 is A21 and x2 is A22 , then y = a21(x1゜) + a22(x2゜) + b2
ルールm:If x1 is Am1 and x2 is Am2 , then y = am1(x1゜) + am2(x2゜) + bm
この形態のファジィ集合は下図に示すような台形型のメンバシップ関数を前件部に用います。
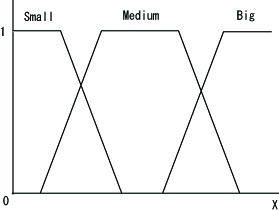
例として次の2つの制御規則を考えてみます。
ルール1:If x1 is A11 and x2 is A12 , then y = a11(x1゜) + a12(x2゜) + b1
ルール2:If x1 is A21 and x2 is A22 , then y = a21(x1゜) + a22(x2゜) + b2
入力x1゜、x2゜に対する前件部の適合度ω1、ω2は、
ω1 = A11(x1゜) ・ A12(x2゜)
ω2 = A21(x1゜) ・ A22(x2゜)
のように、積で定義されます。これに対して、制御ルールに対する後件部の値y1、y2は次のように求められます。
y1 = a11(x1゜) + a12(x2゜) + b1
y2 = a21(x1゜) + a22(x2゜) + b2
高木・菅野のファジィ推論では最終的な推論結果を次式のように重み付き平均をとることで得ます。
戻る 次へ