2.2 ニューロンモデル

ここではMcCullochとPittsが提案したニューロンモデルを図2.2に示す。[3]

  
図 2.2: ニューロンモデル

  

式(2.1)において、 はi番目の入力のシナプス結合の強さを表し、i番目の入力が来ると（すなわち )ニューロンの膜電位が だけ変化することを示す。 が正であれば興奮性シナプスを、負であれば抑制性シナプスを表し、また結合がなければ である。また式(2.1)の はしきい値を表し、各入力にシナプスの重みを掛けた荷重和 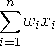がしきい値 を越えたときのみ、ニューロンが興奮して電気パルスを出力する（すなわちy=1）離散時間モデルである。ニューロンモデルは、一種の多数決で出力を決める素子である。ただし、各入力 の一票の重みは であり、この一票の格差を積極的に利用するものである。この際抑制性のシナプスは、マイナスの票を投じることを意味する。

ニューロンモデルの各入力および出力は、1または0の値をとり、1はニューロンが興奮 発火した状態、0は静止状態に各々対応する。 このように、出力として0、1の二値をとるようなモデルを、 入力の総和がしきい値を越えた時のみ1を出力することから、 線形しきい値素子モデルという。

  
図 2.3: ニューロンの出力

 

連続モデルの場合の f[u] の形はいろいろなものが考えられるが、良く使われるのはシグモイド関数と呼ばれるものである。 シグモイド関数として有名なものは、

 

という形のものである。