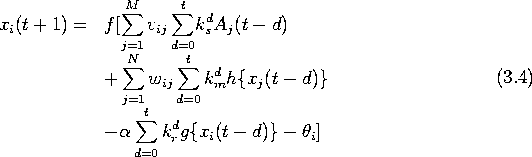
カオスニューロンモデルを相互結合したネットワークをカオスニューラルネットワークと呼んでいる。 M 個の入力と N 個のニューロン間の相互結合を持つカオスニューラルネットワークにおいて、 i 番目のカオスニューロンのダイナミクスは式(3.4)で与えられる[7]。
ここで 
は時刻 t+1 における i 番目 (i=1,2,・・・,N) のニューロンの出力、 f はカオスニューロンの出力関数、 
は j 番目の入力 
から i 番目のニューロンへのシナプス結合係数、 
は時刻 t における j 番目 (j=1,2,・・・,M) の入力の大きさ、 
は j 番目のニューロンから i 番目のニューロンへのシナプス結合値、 h は j 番目のカオスニューロンから i 番目のカオスニューロンへ結線する軸索が有する活動電位の電播に関する変換関数、 g は不応性の特性を表す関数、 
は不応性の項に対するスケーリングファクタ ( 
) 、 
は時間的減衰定数、 
は i 番目のニューロンのしきい値である。
この時、 i 番目のニューロンの内部状態を、外部入力の項 
とニューロン間の相互結合の項 
、そしてニューロン自身の不応性の項 
の三つに分けて考えると式(3.4)は
と表すことができ、それぞれ次のように簡単化できる。
