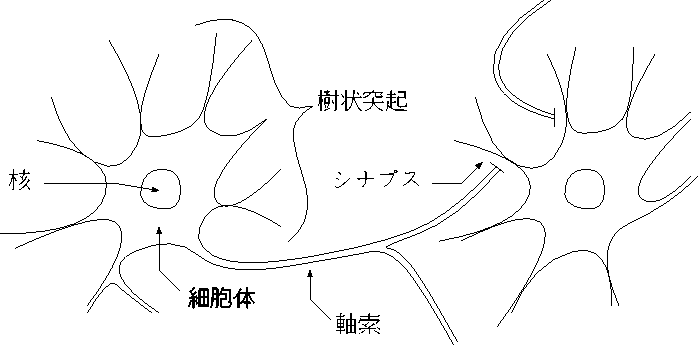
図 2.1: 神経細胞の構造
神経細胞は、図(2.1) のような構造になっている。 この図では細胞が2個しかないが、 実際は、人間の脳の場合100億から1000億程度 あるといわれている。 これらの神経細胞は、3次元に密に結合している。 一つ一つのニューロンは、多数のニューロンの出力を受けとり、シナプスで増減し、 それを足した値がある値を超えると出力し、他の多数のニューロンに伝送する。 その入力部分を樹状突起、出力部分をシナプス、伝送路に当る部分を軸索という。
ニューロンは、神経インパルス(Nervous Impulse)と呼ばれる 電気パルスを生成し、これが出力となる。 このパルス幅は、約1[ms]であり、通常のディジタル電子回路に使われるパルスと 比べると、とても低速である。 このパルスの振幅は、入力値に関わらずほぼ一定である。 では、入力は出力に影響しないのかというと、そうではなく 入力の合計が閾値より小さいと出力はなく、閾値を超えるとパルスを出力する。 この特性は、全か無かの法則(all-or-none law)と呼ばれる。
これをモデル化したものがニューロンである。 これは、 図(2.2) のような構造になっている。
このニューロンの出力は、式(2.1) で表される。
![]() は単位ステップ関数、
は単位ステップ関数、 ![]() は入力の数、
は入力の数、
![]() は
は ![]() 番目のニューロンの出力、
番目のニューロンの出力、 ![]() は
は ![]() 番目のニューロン
から
番目のニューロン
から ![]() 番目のニューロンへの重み、
番目のニューロンへの重み、 ![]() は閾値をあらわす。
は閾値をあらわす。