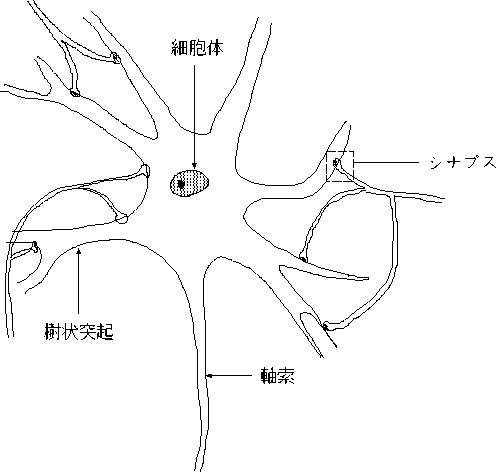
図 2.1: 神経細胞の構造
ニューロンというのは神経細胞モデルのことである。 まず、神経細胞について説明する。 次の図 2.1にニューロンの元である 神経細胞の構造を示す。
神経細胞は図のように、細胞体とそのまわりにある枝わかれした樹状突起と、
軸索、そしてその先にあるシナプスにより構成されている。
この軸索とシナプスにより他の神経細胞と情報のやりとりを行なっている。
このシナプスは1つの神経細胞につき、
![]() 〜
〜 ![]() もの数形成される[1]。
神経細胞は他の神経細胞からの膜電位を計算し、その値と
自らのしきい値を比較し、しきい値よりも膜電位が大きい場合、
一定の大きさの興奮パルスを出して(これを発火という)
その信号をまわりの神経細胞に
シナプス結合を通して送っている [2]。
もの数形成される[1]。
神経細胞は他の神経細胞からの膜電位を計算し、その値と
自らのしきい値を比較し、しきい値よりも膜電位が大きい場合、
一定の大きさの興奮パルスを出して(これを発火という)
その信号をまわりの神経細胞に
シナプス結合を通して送っている [2]。
このシナプス結合には興奮型と抑制型とがあるが、 両者は関与している科学伝達物質の種類により区別されており、 どちらであるかはシナプス結合の送り手である神経細胞により 決まってしまうものであると考えられている(これをデール則という)[3]。 これが神経細胞がつくるネットワークの基本であるとされている。
次に、ニューロンについて説明する。 図 2.2はマッカロ(McCulloch)ピッツ(pitts)形の入出力特性を もつニューロンを表している。
このモデルは、
という3つの条件を満たすように考えてある[4]。 まず、神経細胞は多くの細胞から入力を受けて出力を出すことから、 多入力1出力の素子であると考えられる。他の細胞の出力はシナプス結合を 介して入力として与えられるが、このとき、シナプス前細胞がシナプス後細胞に及ぼす 影響の強さは各細胞によって異なると考えられる。
![]() は入力であり、0か1のパルス信号である。
は入力であり、0か1のパルス信号である。
![]() はそれぞれのシナプス結合の
強さを表すもので、結合荷重と呼ばれるものである。
はそれぞれのシナプス結合の
強さを表すもので、結合荷重と呼ばれるものである。
![]() はニューロンのしきい値を表している。
yはニューロンの出力を表している。
次に、以上の値についての関係式を示す。
はニューロンのしきい値を表している。
yはニューロンの出力を表している。
次に、以上の値についての関係式を示す。
式(2.1)において、uは内部ポテンシャルと呼ばれる。
この式は ![]() という入力が来た場合に、ニューロンの膜電位uが
という入力が来た場合に、ニューロンの膜電位uが ![]() だけ
変化することを示している
だけ
変化することを示している
式(2.3)は、ニューロンからの出力を示しているが、 その値は興奮した状態の出力である1と 興奮していない状態の出力である0との二通りあることを示している。 このようなモデルのことを線形しきい値素子モデルと呼んでいる。
また、連続モデルのf[u]の形はいろいろあるが、 よくつかわれるのはシグモイド(S字形)関数である。 式(2.4)に有名なシグモイド関数を示す。
これまでつかってきた結合荷重 ![]() と膜電位uは一般的に実数値を用いることが
多い。
と膜電位uは一般的に実数値を用いることが
多い。
実際の神経細胞というのは、厳密には出力が完全には0か1にはならない。 出力はその途中のどちらでもない値を経て 連続的に値が変化するのである。