図6.1 に使用するカオスニューラルネットワークの構造を示す。
これは、入力層が音を表すために音の長さと高さで1つずつ、0または1の値を持つニューロンが28個で計30個の素子があり、
中間層は50個で、
出力層は１つの音符を表すために２個、次の１音に対する２値のデータを持つ素子が28個で計30個の素子を使用している。
なお、使用する結合荷重（重み）w、閾値 
は、
ニューラルネットワークに学習させた後の値を使用し、
さらに、カオスニューロンの特徴を決めるパラメータ 
を入力する。
[MIDI]
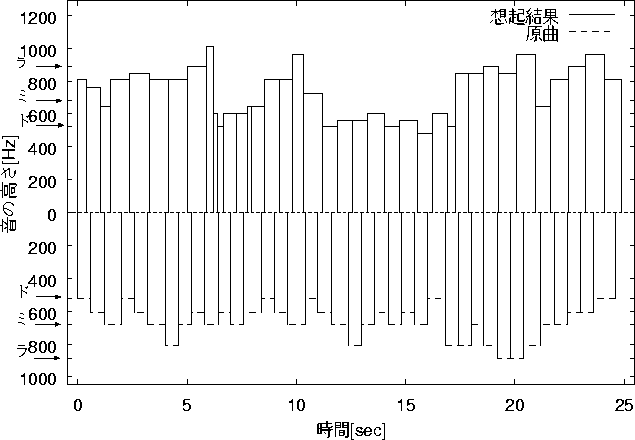
図 6.11: 
=0.526, 
=0.0 
=0.522の想起結果
[MIDI]
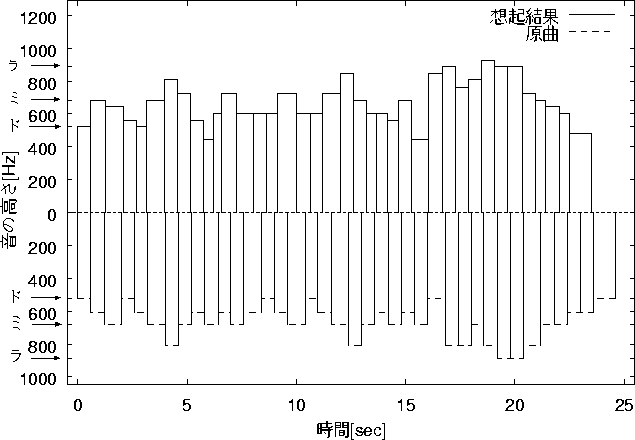
図 6.12: =0.2, =0.2, =0.2の想起結果
[MIDI]
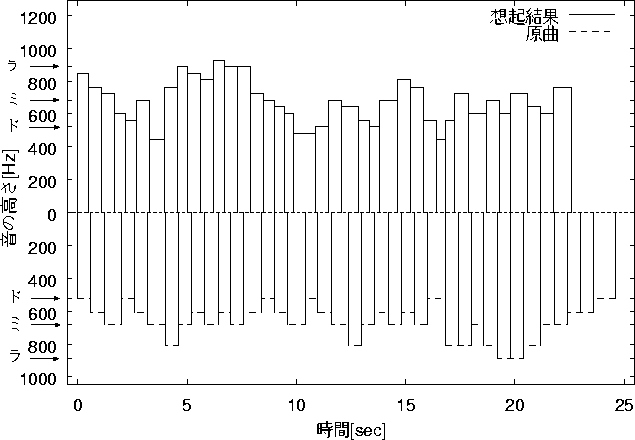
図 6.13: =0.2545, =0.2545, =0.2545の想起結果
入力するパラメータとして、
昨年度カオスニューラルネットワークを用いた想起の際、
パラメータ が
という値において変化がわかりやすい結果が得られたため、
これを用いて10倍、0.1倍、
どれかを0にするなどの組合せによる入力を与える実験を行なう。
この結果の一例として図6.11 を示す。
出力した値より教師信号とは違う新しい曲を想起したといえる。
なお、このときの の値は 
としている。
次に上記で述べたカオスニューラルネットワークの想起結果を受け、
カオスニューロンの特徴を決めるパラメータ の
変化によって曲がどのように変わるかを調べるために、
全てのパラメータを一様に増加させ、各結果を比較していく。
その一つの例として、図6.12 を示す。
このときの の値は 
であり、
この想起結果も教師信号とは違う曲を想起した。
パラメータを増加させていく過程で、
前述の =0.2, =0.2, =0.2 ように各パラメータが
小さい値ではまだ原曲に近い部分が存在するが、
=0.526, =0.0, =0.522 のような
どれかが大きい値では原曲にはほど遠くなる。
また =0.2545, =0.2545, =0.2545 の結果を図6.13 に示す。
この結果では原曲を残した部分が周期がずれて出力されている。
つまりパラメータの変化によって時系列が
周期をずらして想起されることがあるといえる。
この理由としてはパラメータの変化によって音符の値と共に、
２値のデータの内容も変化することによって、
別の音符であると認識されるからであると思われる。
この結果からパラメータの高い領域で出力された曲は全く違うように思われたが、
周期をずらせば原曲に近くなるところもあるかもしれないと推察できる。
また、出力を次の入力としているために実行回数を繰り返すと、 ネットワークの値によって出力が変化して、 さらに原曲とは違った曲を想起すると思われるが、 何度繰り返させても曲に変化は見られない。 これは２値のデータを持つ入力層のネットワークに与える影響が強いために、 音符に対して少しの誤差が生じても、２値のデータに対して誤差が生じないので、 結果として音の値も安定するからである。