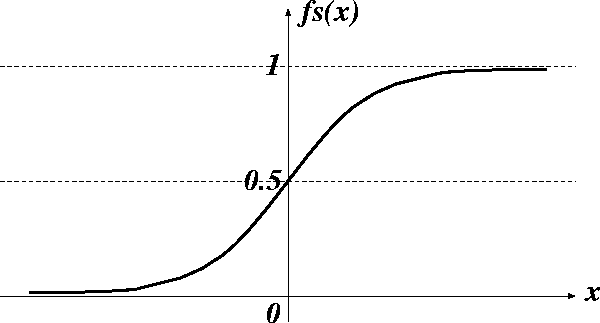
図 3.4: シグモイド関数
カオスニューロンは、ニューロンをより脳内の神経細胞に近付けるため、 いろいろな改良がしてある。
実際の脳内の神経細胞の出力は、全か無かの法則に従わず、 出力にばらつきがある。 そこで、出力関数に単位ステップ関数の変わりに、シグモイド関数を使う。 シグモイド関数は図3.4と式(3.2)で表される。 図3.5は、シグモイド関数を微分した関数を示している。
![]() は、立ち上がりの鈍さを表すパラメータである。
この関数はニューロンにカオスを発生させるために取り入れられたが、
他にも、ニューロンの出力に使われている単位ステップ関数は不連続であるので
微分するとデルタ関数になり、コンピュータでは計算でないが、
シグモイド関数は微分がコンピュータで計算できるという利点がある。
は、立ち上がりの鈍さを表すパラメータである。
この関数はニューロンにカオスを発生させるために取り入れられたが、
他にも、ニューロンの出力に使われている単位ステップ関数は不連続であるので
微分するとデルタ関数になり、コンピュータでは計算でないが、
シグモイド関数は微分がコンピュータで計算できるという利点がある。
もう一つの脳内の神経細胞の特徴に「不応性」がある。 不応性とは、脳内の神経細胞がパルスを発生した直後からしばらくの間は、 パルスを出力しにくくなる性質のことである。
カオスニューロンの出力は式(3.3)になる。
![]() は入力情報を、
は入力情報を、 ![]() は内部状態をそれぞれ表す。
これらを式で示すと、式(3.4)と式(3.5)となる。
は内部状態をそれぞれ表す。
これらを式で示すと、式(3.4)と式(3.5)となる。