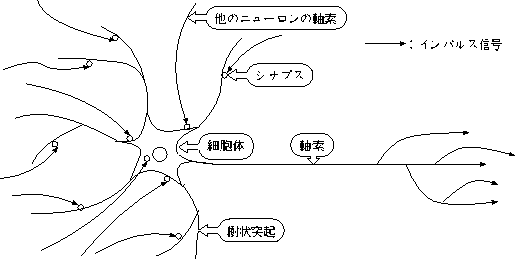
図 2.1: ニューロンの構造
生物の脳は、多数のニューロン(neuron:神経細胞)からなる 大規模ネットワークである。
ニューロンとは外見的に、細胞体(soma)、樹状突起(dendrite)、軸索(axon) の3つの部分に分けられる。 細胞の中央部分に当たるのが細胞体であり、細胞核はこの中にある。 樹状突起は、細胞体の表面から突き出た、多くの枝に分かれた突起のことで、 簡単にいえばニューロンの入力部である。 軸索は、細胞体からほぼ一定の太さで長く伸びた一本の突起で、 信号伝送路のことである。 一般に神経細胞と呼ばれているのは、この軸索である。 軸索の終りに細胞体や樹状突起に付着している部分をシナプス(synapse)という。 軸索は十から数百に分岐しており、シナプスを介して数多くの細胞につながっている。 また、ひとつの細胞が受けるシナプス結合の数は、数百から数万に及ぶ。
生物の脳の内部にはこのニューロンが数千〜数千億個程あり、 互いが3次元的に結合をしている。そしてニューロン同士をシナプスが繋げて、 視覚、聴覚、嗅覚など5感から入ってくる膨大な情報を処理、 出力までの一連の動作をごく僅かな時間の間に行っている[1]。
ニューロンの構造を図 2.1 に示す。
脳の基本素子ニューロンの動作を、ニューロンコンピューティング研究の立場から 一言で表現するば、多入力-1出力の非線形素子ということになるが、 その実体はとても小さな生物分子機構に基づく複雑な高機能素子であり、 たいへん豊富なダイナミックスを有している。
したがって、ニューロンの数学モデルは、定性的で単純なモデルから、 現実の生物のニューロンに近い定量的で複雑なモデルまで、そのスペクトラムが 広い、ニューロンへの多数の入力の時空間加算、ニューロンに特有の閾値作用、 不応性、疲労、可塑性などを、目的に合わせてモデル化する。 このニューロンの動作をモデル化したものをニューロンモデルと呼ぶ[2]。
ニューロンの数学モデル研究の上で、歴史的に重要なニューロンモデルに、
マカロとピッツのモデルのニューロンモデルを図 2.2に示す。
![]() は i 番目のニューロンからの入力で、
ここでは0か1の値をとる。
は i 番目のニューロンからの入力で、
ここでは0か1の値をとる。 ![]() はそのニューロンからの入力のシナプス結合の強さを表す。
はそのニューロンからの入力のシナプス結合の強さを表す。
![]() が正ならばその入力はニューロンを興奮させる方向へ働き、
逆に負であればニューロンの興奮を抑制する働きをする。
前者のシナプス結合を興奮性シナプス、後者を抑制性シナプスと呼ぶ。
i 番目のニューロンと結合していない場合、
が正ならばその入力はニューロンを興奮させる方向へ働き、
逆に負であればニューロンの興奮を抑制する働きをする。
前者のシナプス結合を興奮性シナプス、後者を抑制性シナプスと呼ぶ。
i 番目のニューロンと結合していない場合、 ![]() は0である。
最終的なニューロンの出力 y は、
は0である。
最終的なニューロンの出力 y は、
で表される。式(2.1)において、
f(u) はニューロンの出力関数を表す。
ニューロンへの入力 ![]() とそれぞれに対するのシナプス結合の強さ
とそれぞれに対するのシナプス結合の強さ ![]() との積を合計し、その値から閾値
との積を合計し、その値から閾値 ![]() を引いたものを出力関数に
かけて出力を得る。
を引いたものを出力関数に
かけて出力を得る。
マッカロとピッツのモデルでは 出力関数は式(2.4)のような 線形閾値関数で表される。 この関数は単位階段関数とも呼ばれるもので、 この入出力特性は図 2.3 のようになる。 すなわち入力 u が0を越える場合は出力 y は1となり、 入力が0以下の場合は出力は0となる。
入力の総和から閾値を引いた結果が0より大きければニューロンは興奮して 1を出力し、0以下であればニューロンは静止状態のままで出力は0である。 このようなモデルを線形閾値素子モデルと呼ぶ。
次に、カイアニエロのモデルを式(2.3)に示す。
ここで、