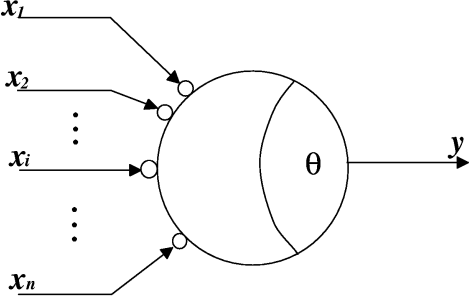
図 2.2: マカロック-ピッツのモデル
ニューロンのモデルとして歴史的に重要なものに、1943年のマカロック-ピッツ (McCulloch-Pitts)のモデルがある。
マカロック-ピッツのモデルを図 2.2に示す。
![]() はi番目のニューロンからの入力、
はi番目のニューロンからの入力、 ![]() はその入力の
シナプス結合の強さであり、i番目のニューロンが及ぼす影響は
はその入力の
シナプス結合の強さであり、i番目のニューロンが及ぼす影響は
![]()
![]() と表される。
と表される。
![]() はニューロンの発火のしきい値である。
以上のことを式で表すと、次のようになる。
はニューロンの発火のしきい値である。
以上のことを式で表すと、次のようになる。
式 (2.2)で表されるuを膜電位、あるいは内部ポテンシャルという。 出力関数f(u)はマカロック-ピッツのモデルでは図 2.3に示す 単位ステップ関数で、次のように表される。
このように、出力として0, 1の2値をとるようなモデルを、入力の線形和
( ![]() )がしきい値(
)がしきい値( ![]() )を越えた時のみ1を出力することから、
線形しきい値素子モデルという。
また、このようにしきい値を境にして、活動電位の発生、非発生が不連続に
分かれるダイナミクスを、全か無かの法則(all-or-none law)という。
)を越えた時のみ1を出力することから、
線形しきい値素子モデルという。
また、このようにしきい値を境にして、活動電位の発生、非発生が不連続に
分かれるダイナミクスを、全か無かの法則(all-or-none law)という。