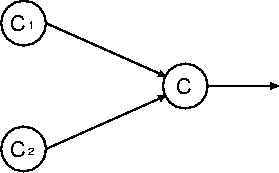
図 4.1: 2入力のニューロン
同期ニューラルネットワークにおける学習の原理を、次の様にする。
これについて詳しく説明するために、図4.1の様な二つのニューロンから 接続されているニューロンを例に挙げる。
このニューロンには図4.2の入力が過去に入ったものとする。
ここでニューロン ![]() からとニューロン
からとニューロン ![]() からの信号の周期を等しく考えるのは、
外部からの入力はどのニューロンにも等しく入力されていてるので、
同期ニューラルネットワークを巡る信号は全てこの外部入力に起因し、
それらの信号の違いは位相だけであると考えられるからである。
からの信号の周期を等しく考えるのは、
外部からの入力はどのニューロンにも等しく入力されていてるので、
同期ニューラルネットワークを巡る信号は全てこの外部入力に起因し、
それらの信号の違いは位相だけであると考えられるからである。
この図より、パルスを出力させるためにはニューロン ![]() の出力を右に、
ニューロン
の出力を右に、
ニューロン ![]() の出力を左にシフトして、ニューロン
の出力を左にシフトして、ニューロン ![]() からと
ニューロン
からと
ニューロン ![]() からのパルスのタイミングを合わせれば良いことがわかる。
ここで出力を右にシフトすることは、信号の到達時間を大きくして信号が
入ってくるタイミングを遅らせることを意味し、出力を左にシフトする
ことは、信号の到達時間を小さくして信号が入ってくるタイミングを早めることを
意味する。
からのパルスのタイミングを合わせれば良いことがわかる。
ここで出力を右にシフトすることは、信号の到達時間を大きくして信号が
入ってくるタイミングを遅らせることを意味し、出力を左にシフトする
ことは、信号の到達時間を小さくして信号が入ってくるタイミングを早めることを
意味する。
しかし、前節でニューロンは時間的にも空間的にも限られた情報しか 参照することは出来ないと述べた。この方法では、ニューロンは空間的には 局所的だが、時間的には遠い過去までの信号を参照していることになる。 そこで、ニューロン内部に新たなパラメータを考え、それによって 同様の結果が導ける様にする。
この新たなパラメータは、接続されているニューロン一つにつき一つ用意され、 そのニューロンからの入力の総和を記憶する。入力の総和は過去のものほど重みが 小さくなる様にする。これを式で表すと
となる。ここでm(t)が入力の総和、s(t)がニューロンからの入力、kは係数で 1未満である。kが1未満であるので過去の入力はkの累乗に比例して 小さくなる。これは過去から現在までの入力に、指数関数的な重みをかけたものの 和に等しい。 これより、ニューロンが入力の総和m(t)の値しか知らない場合についての学習方法を 考えてみる。
今、ニューロン ![]() からの入力の総和
からの入力の総和 ![]() とニューロン
とニューロン ![]() からの
信号の総和
からの
信号の総和 ![]() を比べた時、
を比べた時、 ![]() の方が大きかったとする。
遠い過去に入力された信号の影響は小さく無視出来ると考えられるので、
過去の入力は図4.3の様にニューロン
の方が大きかったとする。
遠い過去に入力された信号の影響は小さく無視出来ると考えられるので、
過去の入力は図4.3の様にニューロン ![]() からの方が
遅く入力されたと予想される。
しかしこれだけの情報では実際の入力が、図4.4の
様にニューロン
からの方が
遅く入力されたと予想される。
しかしこれだけの情報では実際の入力が、図4.4の
様にニューロン ![]() からのパルスが、ニューロン
からのパルスが、ニューロン ![]() からのパルスのすぐ後に
入力されたのか、また図4.5様にューロン
からのパルスのすぐ後に
入力されたのか、また図4.5様にューロン ![]() からのパルスが
入力されてから時間が経った後に入力されたのかはわからない。
パルスが出力されるためには、
図4.4の様ならばニューロン
からのパルスが
入力されてから時間が経った後に入力されたのかはわからない。
パルスが出力されるためには、
図4.4の様ならばニューロン ![]() からの出力を右に、
ニューロン
からの出力を右に、
ニューロン ![]() からの出力を左にシフトした方が良いが、図4.5の
様ならばニューロン
からの出力を左にシフトした方が良いが、図4.5の
様ならばニューロン ![]() からの出力を左に、ニューロン
からの出力を左に、ニューロン ![]() からの出力を右に
シフトした方が良いため、
図4.4、4.5どちらであるかという情報は必要である。
からの出力を右に
シフトした方が良いため、
図4.4、4.5どちらであるかという情報は必要である。
図4.4、4.5のどちらであっても 適した方へシフトさせるために、 入力の総和と信号の到達時間の関係を次の様に定める。
これらの原則によってパルスが出力される様になるまでを、図4.6〜 4.12によって説明する。
これで一周期であるが、全体で見ると、 ![]() は増加、
は増加、 ![]() は
減少している。つまり、よりパルスが出力される様に、発火する様に
変化したと言える。
は
減少している。つまり、よりパルスが出力される様に、発火する様に
変化したと言える。