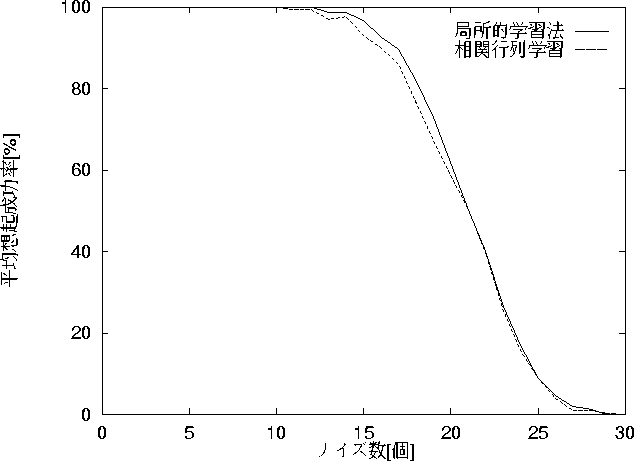
図 5.4: 両学習法のノイズ耐性
図5.4は、ノイズを増やしていった時の学習できたパターンの平均想起成功率である。学習できたパターンの想起成功率の平均をとるのはパターンの似か寄りの関係上ノイズ耐性が各パターン毎に変わるので、その平均をとることで一元的にネットワークのノイズ耐性を調べるためである。
学習できたパターン数はどちらも3個に統一し比較してある。
図を見ると、ノイズの個数が10個までどちらも想起成功率が ![]() を維持しているが、そこから徐々に下がり、
15個を越えると急激に成功率は低下する。ノイズの個数が28個を越えるとどちらも成功率は
を維持しているが、そこから徐々に下がり、
15個を越えると急激に成功率は低下する。ノイズの個数が28個を越えるとどちらも成功率は ![]() となった。
となった。
ノイズ耐性は局所的学習法の方がホップフィールドネットの学習法に比べ若干良いがあまり差がない。 また想起成功率の低下に関してどちらも同じノイズ数から低下し始め、 その低下率もほぼ同じであることから、 この特性は学習法によらずネットワークの構造に起因するものであると考えられる。
次に学習パターンの増加によるノイズ耐性の特性を見る。
図5.5は、局所的学習法における学習済みパターン数によるノイズ耐性の違いのグラフである。各パターンの学習回数は学習個数によらず一律1000回である。
これを見るとパターンの数が10個の時は、ノイズ7個まで成功率 ![]() を維持しているのに対し、パターンの数15個ではノイズ1個の段階で成功率が
を維持しているのに対し、パターンの数15個ではノイズ1個の段階で成功率が ![]() を下回った。
を下回った。
これは大文字のF、Hなど特徴が似た文字が増えたためであると考えられる。
また学習パターン数が25個までをみると、ノイズ25個で想起成功率が ![]() もしくは、ほとんど
もしくは、ほとんど ![]() になっている。
これはニューロン数49個の
になっている。
これはニューロン数49個の ![]() にあたる。
にあたる。
このことからノイズがのっていても入力パターンを想起できる限界が、ニューロン総数の約 ![]() にあることがわかる。これを越えると学習できたパターンを想起することは不可能といえる。
にあることがわかる。これを越えると学習できたパターンを想起することは不可能といえる。
上記の実験において想起成功率が ![]() を下回った時のノイズ数をとったものが図5.6である。
を下回った時のノイズ数をとったものが図5.6である。 ![]() を下回った時の点をとった理由は、今回の実験ではパターン同士の似か寄りを無視し、アルファベット順にパターンを学習させたためそれまでに学習したパターンに似たパターンが新たに学習されれば当然ノイズ耐性は急に悪くなる。
前述したようにパターンを10個学習させた場合と15個学習させた場合の差がそれである。図5.5をみると15個学習させた場合の想起成功率はノイズが数個の時は
を下回った時の点をとった理由は、今回の実験ではパターン同士の似か寄りを無視し、アルファベット順にパターンを学習させたためそれまでに学習したパターンに似たパターンが新たに学習されれば当然ノイズ耐性は急に悪くなる。
前述したようにパターンを10個学習させた場合と15個学習させた場合の差がそれである。図5.5をみると15個学習させた場合の想起成功率はノイズが数個の時は ![]() 付近をうろうろしているが、ノイズが増えると学習できたパターン数が10個の時と同様に成功率が下がり始める。
付近をうろうろしているが、ノイズが増えると学習できたパターン数が10個の時と同様に成功率が下がり始める。
ここではノイズ耐性の一般的な特性を掴みたかったので想起成功率 ![]() を下回った点を抽出した。
を下回った点を抽出した。
これを見るとパターンの数が増加するとノイズ耐性もそれに比例して低下していくが、 パターンの数が学習できる限界に近付くにつれ、ノイズ耐性もある程度以上低下しなくなることがわかる。
図5.7は10個のパターンを学習するのに最低限必要な学習回数200回からさらに学習回数を増やしていった時のノイズ耐性を示したグラフである。
各パターンの学習回数が200回、400回、1000回と増加した時のノイズ耐性は200回学習させた時、ノイズ1個で想起成功率 ![]() を維持できなくなっているのに対し、400回、1000回学習させた時はどちらもノイズ6個で成功率
を維持できなくなっているのに対し、400回、1000回学習させた時はどちらもノイズ6個で成功率 ![]() を維持できなくなり、ノイズ28個で成功率が
を維持できなくなり、ノイズ28個で成功率が ![]() になるなど、全く同じ特性示している。
になるなど、全く同じ特性示している。
これは学習回数が400回の時点で各パターンを完全に学習しきり他のパターンとの区別が完璧に行なえるようになったためにそれ以上学習回数が増えても特性が変化しなかったと考えられる。
ノイズ耐性の面から見ると、学習回数が200回に比べ400回以上では成功率 ![]() を維持できるノイズ数が増えたことから、学習回数の増加によるノイズ耐性の上昇を見込めることがわかる。しかし、それも各パターンを完全に学習する回数までである。
を維持できるノイズ数が増えたことから、学習回数の増加によるノイズ耐性の上昇を見込めることがわかる。しかし、それも各パターンを完全に学習する回数までである。
図5.8は学習回数を各パターン1000回一定とし、結合荷重の変位を変化させ10個のパターンを学習させた時のノイズ耐性を示したグラフである。
結合荷重の変位が±0.10の時と±0.05の時とを見比べてみると、どちらもノイズ数7個で想起成功率が ![]() を維持できなくなり、ほぼ同じ割合で成功率が低下していきノイズ数27個で成功率は
を維持できなくなり、ほぼ同じ割合で成功率が低下していきノイズ数27個で成功率は ![]() となっている。
となっている。
この結合荷重の変位による特性の違いは非常に小さいので誤差といえる。
つまり二つの特性に違いがないことから、結合荷重の変位が十分に小さいならば変位をそれ以上小さくしてもそのノイズ耐性に大きな違いは生まれないことがわかる。
以上のことを踏まえれば、図5.4で大きな差が生じなかったのは、 比較に使用したホップフィールドネットの学習法の学習できたパターンがあまりに少なかったため、ノイズが多少入っても容易に入力パターンが想起出来たと考えられる。
局所的学習法では結合荷重の変位を任意に設定できるがノイズ耐性の面からは相関行列に基づくホップフィールドネットの学習法と大差ないといえる。
学習パターンが増えればノイズが入るとパターンを区別することが困難になるため、学習回数を増やすことによりノイズ耐性を上げることが出来るという点で前節同様に局所的学習は優れているといえる。