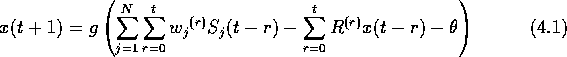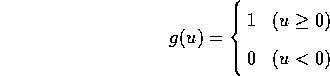


Next: 4.2 カオスニューロンのダイナミクス
Up: 第4章 カオスニューロン
Previous: 第4章 カオスニューロン
ニューロンの数学モデル研究の上で、
歴史的に重要なモデルの一つに
``カイアニエロ(Caianiello)のモデル''がある。
本研究では、
このカイアニエロのモデルを用いてニューラルネットワークを構成する。
[6]
脳の基本素子であるニューロンの動作を、
ニューロコンピューティング研究の立場から一言で表現すれば
``多入力−1出力の非線形素子''ということになるが、
その実態は精密な生体分子機構に基づく複雑な高機能素子である。
したがってニューロンの数学モデルは、
定性的で単純なモデルから現実の生物のニューロンに近い定量的で複雑なモデルまで、
そのスペクトラムは広い。ニューロンへの多数入力の時空間加算、
ニューロンに特有のしきい値作用、不応性、疲労、可塑性など何を目的として、
どのようにモデル化するかが問題となる。
以下にそれらのうち、時空間加算としきい値作用と不応性を考慮した例である
カイアニエロのモデルを示す。
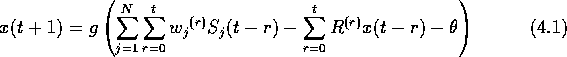
- x(t+1)
- : 時刻 t+1 のニューロンの出力値、出力は、1(発火状態)
または0(非発火状態)のいずれかである。また、時間は離散的に刻まれる。
- g
- : 単位ステップ出力関数
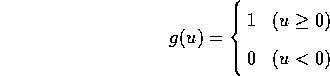
- N
- : ニューロンへの入力線の総数。
-
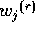
- : 時刻 t-r における j 番目の
入力値
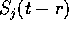 (1または0の値をとる)が、
時刻 t+1 でのニューロンの出力値へ与える影響の強さを表すシナプス結合係数。
(1または0の値をとる)が、
時刻 t+1 でのニューロンの出力値へ与える影響の強さを表すシナプス結合係数。
-
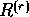
- : 時刻 t-r でのニューロンの出力値が、時刻 t+1 でのニュ
ーロンの出力値へ与える影響の強さを表す係数。生物のニューロンにおける不応性
(ニューロンの発火後、一時的にしきい値が増加する性質)に対応する。
-
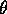
- : ニューロンのしきい値。
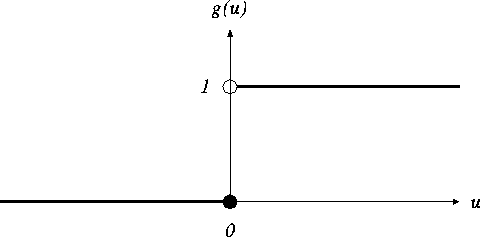
図 4.1: 単位ステップ関数
ここで、これらのモデルは、いずれも図 4.1 で表される出力関数が
不連続な単位ステップ関数であり、
ニューロンの出力は、1又は0の2値である。
このようにしきい値を境にして、活動電位の発生、
非発生が不連続にわかれるダイナミクスを``全か無かの法則''と呼んでいる。
Deguchi Toshinori
1997年03月04日 (火) 08時34分02秒 JST