実験結果

表 6.3: Experiment Result 2

Number	0.8*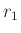$r_1$	0.8*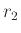$r_2$	0.8*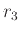$r_3$	$2*\cos (\mbox{step}/ \pi )$	$2*\sin (\mbox{step}/ \pi )$
1	◯:3,820	◯:2,637	◯:2,763	×:55,930	◯:4,295
2	×:33	×:1,345	◯:44	×:2,426	×:108
3	◯:20,786	◯:889	◯:21,797	◯:10,501	◯:59,134
4	×:16381	◯:378	◯:1,961	×:87,340	◯:545,091
5	◯:38,908	◯:35,596	◯:1,911	◯:51,980	◯:605
6	◯:935	◯:5,192	◯:20,907	◯:51,191	◯:284
7	◯:3,891	◯:1,948	◯:8,584	◯:69,257	◯:17,975
8	◯:501	◯:6,158	◯:4,350	◯:13,861	×:36,235
9	◯:1,796	◯:755	◯:7,472	◯:241	◯:15,310
10	◯:278	◯:623	◯:173	◯:2,606	◯:39
11	◯:5,708	◯:21,306	◯:13,615	◯:30,831	◯:23,074
12	◯:311	◯:978	◯:6,034	◯:1,031	◯:23,945
13	◯:19,511	◯:23,452	◯:841	◯:28,191	◯:12,921
14	◯:1,655	◯:1,465	◯:556	◯:25,291	◯:1,078
15	◯:7,117	◯:42,733	◯:5,525	◯:13,794	◯:27,744
16	◯:11,538	◯:12,257	◯:6,190	×:19,518	◯:881
17	◯:1,016	◯:3,522	◯:4,066	◯:38,686	◯:26,959
18	◯:3,740	◯:775	◯:3,543	◯:4,913	◯:17,852
19	◯:3,468	◯:1,660	◯:5,972	◯:10,445	◯:196,225
20	◯:0	◯:0	◯:0	◯:0	◯:0
Success raet[%]	90	95	100	80	90

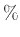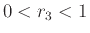記憶させるパターン数が20種類の場合の記憶検索の結果を、Table 6.3に示す。実験1での結 果を元に、特徴抽出機構の学習回数を増やしたため、パターン数が増加したのにも関わらず、記 憶検索の成功率は全て80$\%$を超えている。特に乱数を用いた場合の成功率は三角関数を用い た場合の成功率よりも高く、乱数の範囲が$0 < r_3 < 1$の時には100%となっている。

実験1のTable 6.2と比較して、実験2のTable 6.3は、検索終了までに必要とする時間が 極端に多くなっているところが目立つ。これは、記憶しているパターン数が増えるほど動的に想 起することが難しくなるというカオスニューラルネットワークの性質からも容易に想像できるが 、シナプス前抑制関数に乱数や三角関数を用いることで、そのような動的想起しづらいパターン でも想起させることができるということがわかった。

ここまでの結果で、従来のシナプス前抑制関数の抑制値に乱数を加えるか、三角関数を用いた場合に、記憶検索の成功率が上がることがわかった。続いて、パターン数を30に増やした場合の記憶検索の成功率を調べ、その結果を元に最も有効であると思われる抑制値を絞りたい。