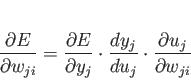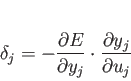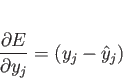


Next: バックプロパゲーション
Up: 学習法
Previous: 学習法の分類
目次
本研究におけるニューラルネットワークの学習は、
バックプロパゲーション法(back-propagation、誤差逆伝搬法)を用いた。
まずバックプロパゲーションについて説明する前に、一般化デルタルールについて説明する。
ある素子 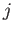 の入力総和
の入力総和 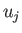 は、
他の素子
は、
他の素子 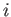 の出力
の出力 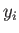 と、重み
と、重み 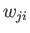 をかけて加えたものである。
また、出力
をかけて加えたものである。
また、出力 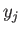 は入力の総和を単調増加関数
は入力の総和を単調増加関数 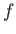 に代入したもので表されることにする。即ち、
に代入したもので表されることにする。即ち、
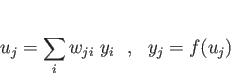 |
(4.1) |
と表せる。ただし、閾値は重みの一つとして含まれていると考える。
ここで、出力関数 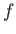 はシグモイド関数を用いることにする。
これは微分可能な関数であり、解析的に問題を解くことが可能になるからである。
はシグモイド関数を用いることにする。
これは微分可能な関数であり、解析的に問題を解くことが可能になるからである。
次に、神経回路における学習を一般化して考える。
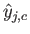 はある入力
はある入力 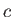 に対して出力素子
に対して出力素子 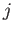 が出すべき望ましい出力、
が出すべき望ましい出力、
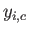 はその時の出力素子が実際にした出力である。
この時の学習評価として、次のような「誤差関数
はその時の出力素子が実際にした出力である。
この時の学習評価として、次のような「誤差関数  」
」
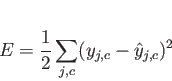 |
(4.2) |
を考える。このような形の誤差関数を最小にする手続きを一般に
「最小2乗平均誤差法」(least mean square、LMS)という。
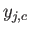 はその時の素子間の結合の強さ、 すなわち重み
はその時の素子間の結合の強さ、 すなわち重み 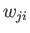 で決まるため、
誤差関数も重みに関して陰(implicit)に定義された関数となる。
したがって、各重みの値を軸としてできる空間を考え、さらにこの誤差関数
で決まるため、
誤差関数も重みに関して陰(implicit)に定義された関数となる。
したがって、各重みの値を軸としてできる空間を考え、さらにこの誤差関数
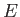 によって定義される値を高さと考えれば、
によって定義される値を高さと考えれば、
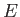 は重み空間上の超曲面として「誤差曲面」を与えることになる。
任意の重み状態から、この誤差曲面の極小値に達するには、
例えば各重みを、
は重み空間上の超曲面として「誤差曲面」を与えることになる。
任意の重み状態から、この誤差曲面の極小値に達するには、
例えば各重みを、
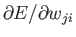 に比例した量
に比例した量
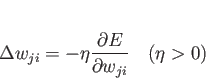 |
(4.3) |
ずつ変化させていけばよいことになる。
ここで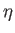 は学習定数である。
これは誤差曲面上を最も急な傾斜方向に進んでいくことに相当し、
このような学習則を一般に「最急降下法」(gradient decent method)という。
は学習定数である。
これは誤差曲面上を最も急な傾斜方向に進んでいくことに相当し、
このような学習則を一般に「最急降下法」(gradient decent method)という。
さて、式 4.1のように素子の性質が定義されていれば、
式 4.3は合成関数の微分公式により、
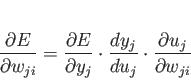 |
(4.4) |
と展開できる(添字  は省略)。
ここで、素子
は省略)。
ここで、素子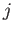 に関する誤差項を
に関する誤差項を 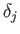 とすれば、
とすれば、
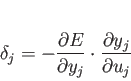 |
(4.5) |
式 4.1を微分して代入すれば、
式 4.3は、
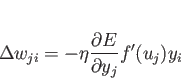 |
(4.8) |
となる。中間層が学習しない場合、
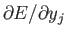 の項は
式 4.2を微分することにより簡単に
の項は
式 4.2を微分することにより簡単に
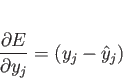 |
(4.9) |
となり、よって
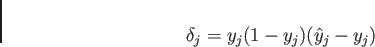 |
(4.10) |
と求めることができるので、式 4.8より、
 |
(4.11) |
という学習則が得られる。
これを一般化デルタルールと呼ぶ。



Next: バックプロパゲーション
Up: 学習法
Previous: 学習法の分類
目次
Deguchi Lab.
2012年3月9日
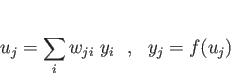
![]() はある入力
はある入力 ![]() に対して出力素子
に対して出力素子 ![]() が出すべき望ましい出力、
が出すべき望ましい出力、
![]() はその時の出力素子が実際にした出力である。
この時の学習評価として、次のような「誤差関数
はその時の出力素子が実際にした出力である。
この時の学習評価として、次のような「誤差関数 ![]() 」
」