


Next: 遺伝的アルゴリズム[8]
Up: 学習法
Previous: 一般化デルタルール
目次
今度はいくつかの中間層を持つ階層型のネットワークを考える。
同じ層の素子間に結合はなく、
どの素子も1つ前の層からのみ入力を受け、
次の層へのみ出力を送るものとする。
このようなネットワークの中間層に対して学習則を導くとき、
式 4.8の
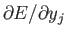 (学習信号)の値は
すぐには求めることが出来ない。
そのため、この学習信号を出力層から逆向きに順々に計算していく。
すなわち出力の誤差を前の層へ、前の層へと伝えていく。
これがバックプロパゲーションの考え方である。
よって、
ある層の素子
(学習信号)の値は
すぐには求めることが出来ない。
そのため、この学習信号を出力層から逆向きに順々に計算していく。
すなわち出力の誤差を前の層へ、前の層へと伝えていく。
これがバックプロパゲーションの考え方である。
よって、
ある層の素子 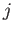 の
の
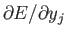 の計算は、
次の層の素子
の計算は、
次の層の素子 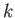 の
の
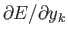 を用いて
を用いて
と展開することができる。
式 4.1より
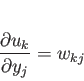 |
(4.14) |
となる。そして、これと式 4.7を
代入すれば式 4.13は
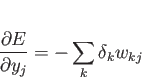 |
(4.15) |
となる。
これがバックプロパゲーションのアルゴリズムである。
バックプロパゲーションは、いかなる重みの初期値からでも誤差が極小となる
(最小ではない)ことが保証されるわけだが、一般に誤差曲面は
極小値の近くでは非常に緩やかな谷底をもつため、学習は非常に遅くなる。
しかし、式 4.3の 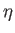 を大きくすると、学習は振動してしまう。
振動させずに学習を早めるため幾つかの方法が提案されているが、例えば、
誤差曲面の傾きを結合荷重空間の位置でなく速度の変化に用いる。
即ち、
を大きくすると、学習は振動してしまう。
振動させずに学習を早めるため幾つかの方法が提案されているが、例えば、
誤差曲面の傾きを結合荷重空間の位置でなく速度の変化に用いる。
即ち、
という形の加速法がよく使われる。
ここで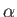 は安定化定数であり、
は安定化定数であり、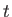 は学習の回数を表わす。
また、重みが最初、すべて0であると、中間層の素子に個性が現れず、
中間層を用いる意味がなくなってしまう。
この対称性を破るために、重みに小さなランダム値を与えることが必要である。
は学習の回数を表わす。
また、重みが最初、すべて0であると、中間層の素子に個性が現れず、
中間層を用いる意味がなくなってしまう。
この対称性を破るために、重みに小さなランダム値を与えることが必要である。
図 4.1 に
バックプロパゲーション法のネットワーク図を示す。
バックプロパゲーションの特徴としては、
図 4.1:
バックプロパゲーション(誤差逆伝搬法)
|
|
- 入力信号と正確な出力教師信号のセットを次々と与えるだけで、
個々の問題の特徴を抽出する内部構造が、
中間層の隠れニューロン群のシナプス結合として自己組織化される。
- 誤差計算が出力方向への情報の流れと類似している。
ということが挙げられる。
すなわち、ある素子の学習に使われている情報は、
後の素子から得られる情報のみであり、学習の局所性が保たれていることになる。
この学習の局所性は、人工的な神経回路型計算機をハードウェア化する時の
学習則に要求される性質である。実際の生体における神経回路においては、
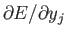 といった学習信号が神経軸索を通って逆向きに伝わることはなく、
バックプロパゲーションは実際の脳の学習則の生理学的モデルには
なりえないことになる。
実際の脳の多層神経回路において、どのような学習則が用いられているのかは
今だ解明されていない。
といった学習信号が神経軸索を通って逆向きに伝わることはなく、
バックプロパゲーションは実際の脳の学習則の生理学的モデルには
なりえないことになる。
実際の脳の多層神経回路において、どのような学習則が用いられているのかは
今だ解明されていない。
Deguchi Lab.
2012年3月9日
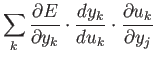
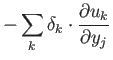
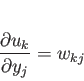
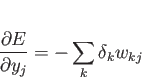
![]() を大きくすると、学習は振動してしまう。
振動させずに学習を早めるため幾つかの方法が提案されているが、例えば、
誤差曲面の傾きを結合荷重空間の位置でなく速度の変化に用いる。
即ち、
を大きくすると、学習は振動してしまう。
振動させずに学習を早めるため幾つかの方法が提案されているが、例えば、
誤差曲面の傾きを結合荷重空間の位置でなく速度の変化に用いる。
即ち、