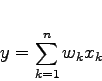 |
(1) |
これらの機能を満たすモデルとして、McCullochとPittsは式(2.1)〜式(2.3)で表される形式ニューロンというモデルを提案した。これを図示すると図 2.2のようになる。
このモデルでは、神経細胞の位置関係や構造、シナプスの構造および機能などの影響因子で決まる神経細胞間の信号の伝わり方を、シナプス結合荷重というパラメータに押し込めて表現している。シナプス前細胞![]() から神経細胞への出力
から神経細胞への出力![]() に比例する入力が神経細胞へ与えられると仮定して、その比例定数をシナプス結合荷重
に比例する入力が神経細胞へ与えられると仮定して、その比例定数をシナプス結合荷重![]() と呼ぶと考えればよい。ある1つの神経細胞から複数の軸索が別の1つの神経細胞に伸びてシナプス結合している場合は、各シナプスの効果すべてを1つのシナプス結合荷重で表すと考えればよい。
と呼ぶと考えればよい。ある1つの神経細胞から複数の軸索が別の1つの神経細胞に伸びてシナプス結合している場合は、各シナプスの効果すべてを1つのシナプス結合荷重で表すと考えればよい。
このモデルが、後のニューラルネットワークの研究の基礎となっている。形式ニューロンでは、入力側神経細胞の膜電位の変化を、シナプス前細胞の出力
![]() の重み付きの和と単純化しており、この重み付きの和がしきい値を超えると、入力側神経細胞が興奮して入力を受けた細胞が出力を出す。式(2.2)がこれを表しており、このステップ関数を用いた出力で全か無の法則を実現している。
の重み付きの和と単純化しており、この重み付きの和がしきい値を超えると、入力側神経細胞が興奮して入力を受けた細胞が出力を出す。式(2.2)がこれを表しており、このステップ関数を用いた出力で全か無の法則を実現している。
その後の研究では入出力関数![]() として、式(2.2)(図 2.3)で示されたステップ関数の代わりに、全領域で微分可能であり、かつ常に有限な出力を出す、式(2.4)で表されるシグモイド関数がよく用いられるようになる。
として、式(2.2)(図 2.3)で示されたステップ関数の代わりに、全領域で微分可能であり、かつ常に有限な出力を出す、式(2.4)で表されるシグモイド関数がよく用いられるようになる。