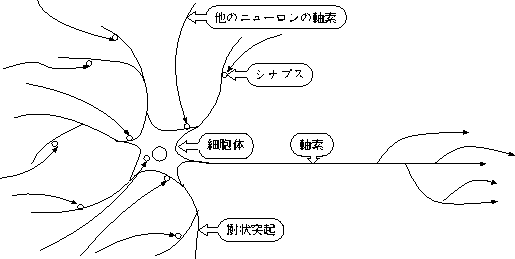
図 2.1: ニューロンの構造
生物の脳神経系を構成している基本素子をニューロン(neuron)と呼ぶ。 生物の脳はこのニューロンが数10億〜数1000億個程3次元的に結合して、 視覚、聴覚、嗅覚など五感からはいってくる膨大な情報を処理し、 出力するまでの一連の動作を僅かな時間の間に行なっている。 [2] ニューロンの構造を図 2.1 に示す。
ニューロンは、入力部の樹状突起(dendrite)と伝送路の軸索(axon)を持ち、 軸索と樹状突起の間で信号のやりとりをする部分をシナプス(synapse)と呼ぶ。
1個のニューロンは他の多数のニューロンからの入力を合計して、 その値がある閾値(threshold)以上の時、神経インパルスと呼ばれる ある一定の大きさの電気パルスを出力する。この時ニューロンは「興奮した」といい、 神経インパルスは軸索を伝わり、シナプスを介して他のニューロンの入力となる。 一方、入力の合計が閾値を越えなかった場合、ニューロンは何も出力しない。 このように、ニューロンの動作は全か無の法則(all-or-none low)に従うと言える。
このニューロンの動作をモデル化したものをニューロンモデルと呼ぶ。 1943年、マッカロ(McCulloch)とピッツ(Pitts)によってニューロンの数理 モデルが提案された [1]。
図 2.2 において、 ![]() は i 番目のニューロンからの入力で、
ここでは0か1の値をとる。
は i 番目のニューロンからの入力で、
ここでは0か1の値をとる。 ![]() はそのニューロンからの入力のシナプス結合の強さを表す。
はそのニューロンからの入力のシナプス結合の強さを表す。
![]() が正ならばその入力はニューロンを興奮させる方向へ働き、
逆に負であればニューロンの興奮を抑制する働きをする。
前者のシナプス結合を興奮性シナプス、後者を抑制性シナプスと呼ぶ。
i 番目のニューロンと結合していない場合、
が正ならばその入力はニューロンを興奮させる方向へ働き、
逆に負であればニューロンの興奮を抑制する働きをする。
前者のシナプス結合を興奮性シナプス、後者を抑制性シナプスと呼ぶ。
i 番目のニューロンと結合していない場合、 ![]() は0である。
最終的なニューロンの出力 y は、
は0である。
最終的なニューロンの出力 y は、
で表される。式(2.1)において、
f(u) はニューロンの出力関数を表す。
ニューロンへの入力 ![]() とそれぞれに対するのシナプス結合の強さ
とそれぞれに対するのシナプス結合の強さ ![]() との積を合計し、その値から閾値
との積を合計し、その値から閾値 ![]() を引いたものを出力関数に
かけて出力を得る。
を引いたものを出力関数に
かけて出力を得る。
マッカロとピッツのモデルでは 出力関数は式(2.3)のような 線形閾値関数で表される。 この関数は単位階段関数とも呼ばれるもので、 この入出力特性は図 2.3 のようになる。 すなわち入力 u が0を越える場合は出力 y は1となり、 入力が0以下の場合は出力は0となる。
入力の総和から閾値を引いた結果が0より大きければニューロンは興奮して 1を出力し、0以下であればニューロンは静止状態のままで出力は0である。 このようなモデルを線形閾値素子モデルと呼ぶ。