素子数と入力パターンの比率による学習の変化

素子数100の時の、1と-1の比率を30:70、40:60、49:51にし、乱数の種を変えて3回行った。 この場合の学習成功数をそれぞれ図 5.3、図 5.4、図 5.5、図 5.6、図 5.7、図 5.8、図 5.9、図 5.10、図 5.11 に示す。なお、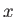$x$軸は入力パターン数、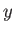$y$軸は学習成功数を表す。

図 5.3: 比率30:70の場合の学習成功パターン数1

図 5.4: 比率30:70の場合の学習成功パターン数2

図 5.5: 比率30:70の場合の学習成功パターン数3

図 5.6: 比率40:60の場合の学習成功パターン数1

図 5.7: 比率40:60の場合の学習成功パターン数2

図 5.8: 比率40:60の場合の学習成功パターン数3

図 5.9: 比率49:51の場合の学習成功パターン数1

図 5.10: 比率49:51の場合の学習成功パターン数2

図 5.11: 比率49:51の場合の学習成功パターン数3

この図から、学習成功数は50:50と結果が異なることが分かる。 どちらも途中までは入力パターン数と学習成功数は同じ関係にあったが、 やはり一定のところから学習成功数は減少し、完全に想起することができなくなっている。 50:50と異なるのは、今回の場合、 完全に想起できなくなったところから減少し、学習成功数は5程度まで落ち込むところにある。 また、30:70、40:60、49:51ともに完全想起が途切れたところから急激に減少していることが分かる。 完全に想起できる最大値を比較してみると、40:60よりも30:70の方が、40:60の時よりも49:51の方が学習できている数が多いことが分かる。 1と-1の比率が49:51の場合は、50:50の時の比率と類似しているため、 想起成功数が増えたと考えられる。

そこで、49:51の場合、パターン数を増やしたときに50:50の結果と類似する可能性があることから、 パターン数を600まで増やして調べることにした。この時の結果を図 5.12に示す。

図 5.12: 比率49:51 パターン数を600まで増やした場合の学習成功数

結果として、パターン数を600まで増やしても学習成功数は増加せず、学習成功数は5前後のままであった。このことから、素子数が100のとき、パターン数を増やし続けたときに完全に想起が可能になるのは50:50の時のみと考えられる。