パーセプトロン

ニューラルネットワークの構造を説明する前にその基となったパーセプトロンについて説明する。 パーセプトロンとは、Rosenblattによって発明され、学習機械の基礎となったネットワークであり、それはMacCullochとPittsの数理モデルを採用したニューロンで構成される[3][4]。

図 3.1: (a) 多層パーセプトロン

図 3.2: (b) 階層型ネットワーク

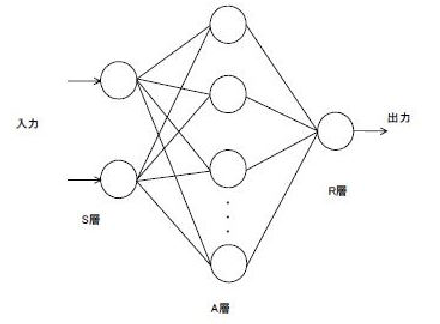
パーセプトロンの構造を図 3.1に示す。パーセプトロンは3層からなるネットワークである。 その層は $S$ 層(Sensory unit)、$A$ 層(Associative unit)、および $R$ 層(Response unit)と呼ばれる。 ネットワークの入力から出力にいたるまで、信号の流れは単一方向である。また各層のニューロン数は制限されない。 $S$ 層は入力信号をそのまま通過させるニューロンである。$A$ 層と$R$ 層のニューロンは活性化関数としてステップ関数を持つマカロック・ピッツモデルである。 このようにフィードバックや相互結合を持たないようなネットワークは一般的に階層構造ネットワークと呼ばれる。 したがって、パーセプトロンは図 3.2のような階層構造ネットワークの一つである。 階層型は、入力層と中間層、そして出力層で構成される。 各層の ニューロン数に制限はなく、中間層の層数も制限は無い。

信号の流れを説明する。まず入力信号はS層を通過し、$S$ 層からの信号を$A$ 層に伝達するが、このとき$S$ 層と$A$ 層の結合に重みがかかっている。 $A$ 層のニューロンでは、$S$ 層の出力とこの重みの加重和がとられ、その和と閾値を比較することで出力を得る。

こうして得た $A$ 層の出力が$R$ 層の入力となるが、$R$ 層への入力は、$A$ 層と$R$ 層の結合の重みの加重和と閾値の比較で$R$層のニューロンの出力が決定され、その値がネットワークの出力値となる。図 3.3と図 3.4にネットワークの計算例を示す。

図 3.3は $S$ 層から $A$ 層の計算、図 3.4は $A$ 層から $R$ 層の計算を示している。 ネットワークは $S$ 層、$A$ 層、$R$ 層はそれぞれ3つのニューロンで構成されている。また $A$ 層と $R$ 層の活性化関数の閾値は0であるとする。

今S層( $S_1$、$S_2$、$S_3$ )に101という入力を与えたとする。S層のニューロンは入力値をそのまま出力する。 この値が $A$ 層( $A_1$、$A_2$、$A_3$ )の入力となる。 図 3.3 は $A_1$ のみの計算を示している。$S$ 層と $A_1$ の結合の重みが $-3.7$, $0.7$, $4.1$ である。

その結果、加重和 $\sigma$ は

$$\sigma = { 1 \times (-3.7)} + { 0 \times 0.7} +{ 1 \times 4.1} = 0.4$$ (3.1)

となる。$\sigma$ は閾値を上回っているので、$A_1$ の出力は1となる。$A_2$ と $A_3$ の出力も同様に求められる。

図 3.4は $R$ 層にあるニューロン $R_1$ についての計算例を示している。 $A_1$ を求めたものと同様に $A_2$、$A_3$ を求め、その結果 $A$ 層( $A_1$、$A_2$、$A_3$ )の出力がそれぞれ $110$ となったと仮定する。 この値が $R$ 層の入力となり、$A$ 層と $R$ 層の結合の重みの加重和と閾値で $R$ 層の出力を決定する。

図 3.4において、$A$ 層と $R_1$ の結合の重みが $2.0$, $-3.6$, $1.9$ であるとすると、加重和 $\sigma$ は

$$\sigma = { 1 \times (2.0)} + { 1 \times -3.6} +{ 0 \times 1.9} = -1.6$$ (3.2)

となり、閾値を下回るのでニューロン $R_1$ の出力は0となる。$R_2$ と $R_3$ も同様にして求められる。

図 3.3: S層からA層の計算

図 3.4: A層からR層の計算

本実験では学習させる対象として時系列を用いているが、 時系列は過去の情報から未来の情報が決定し、 その情報でさらに次の未来の情報を決定するという時間的な方向性を持つ。 そのため、結合の形状に方向性のある 階層型のネットワークを使うこととした。