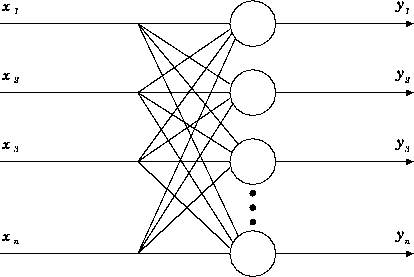
図 5.1: 連想記憶をする神経回路網の構造
人間の記憶は連想である。すなわち、記憶の一部から関係の深いより多くの事柄を想起できる。例えば、ある曲の数小節を聞いただけで、情景、音、においなどの感覚的な経験を完全に思い出すことができる。これが、連想記憶である。
ニューラルネットにおける連想記憶とは、一般につぎのようなものである。
図5.1の様に1つのニューロンに入力 ![]() を全結合させたニューラルネットを考える。
入力パターン
を全結合させたニューラルネットを考える。
入力パターン ![]() と、
出力パターン
と、
出力パターン ![]() の組が複数個
の組が複数個
![]() あるとする。
なお、n はパターンの要素の数であり、要素は全て1と -1 の2値で表される。
ここで、p 個の入力パターンのうち一つをニューラルネットに入力したときに、対応する出力パターンを出力するように、上記の入出力パターンを記憶することを連想記憶という。
あるとする。
なお、n はパターンの要素の数であり、要素は全て1と -1 の2値で表される。
ここで、p 個の入力パターンのうち一つをニューラルネットに入力したときに、対応する出力パターンを出力するように、上記の入出力パターンを記憶することを連想記憶という。
具体的には、まず i 番目の入力から j 番目の細胞へのシナプス荷重 ![]() を全て0にする。
入力と出力の組を与えるとき、以下の学習則に従ってシナプス荷重を更新する。
を全て0にする。
入力と出力の組を与えるとき、以下の学習則に従ってシナプス荷重を更新する。
ただし、閾値 ![]() は 0 とする。これをベクトルで表せば次式となる。
は 0 とする。これをベクトルで表せば次式となる。
これは、入力 x を受けて出力
を出す神経細胞で、情報源 I から信号 ![]() と教師信号
と教師信号 ![]() を受けて学習する場合である。
シナプス荷重
を受けて学習する場合である。
シナプス荷重 ![]() の方程式は式(4.5)より
の方程式は式(4.5)より
で、I の中では信号は等確率で出現するため、平均学習方程式は
で、シナプス荷重は
に収束する。これをベクトル全体で考えるには ![]() を縦に並べたベクトルを
y とし、横ベクトル
を縦に並べたベクトルを
y とし、横ベクトル ![]() を縦に並べたものを行列 W とすれば 式(5.2)となる。
またこれは、ニューロンが同じ状態にあった場合
を縦に並べたものを行列 W とすれば 式(5.2)となる。
またこれは、ニューロンが同じ状態にあった場合 ![]() はシナプス荷重が増加し、そうでない場合にはシナプス荷重が減少するというHebbの変形学習則そのものである。
このようにして学習し、その後、入力 x を与えたときの
出力 y は
はシナプス荷重が増加し、そうでない場合にはシナプス荷重が減少するというHebbの変形学習則そのものである。
このようにして学習し、その後、入力 x を与えたときの
出力 y は
となる。
入力 x が学習したパターンの1つである ![]() の場合、
の場合、
![]() が互いに直交していれば、式(5.8)で
が互いに直交していれば、式(5.8)で
![]() は0となるので、
は0となるので、
![]() となり、
これを単位ステップ関数にいれて2値化すれば
となり、
これを単位ステップ関数にいれて2値化すれば ![]() となるため、
学習した入力に対応したパターンを正しく想起していることが分かる。
となるため、
学習した入力に対応したパターンを正しく想起していることが分かる。
x が ![]() に近いパターン
に近いパターン
![]() の場合、
の場合、
![]() が互いに直交していれば
が互いに直交していれば
![]() は
は
![]() に非常に近い。
一方、
に非常に近い。
一方、 ![]() の
の ![]() とは直交に近い関係にあるのでこれらの項は小さい。
これが十分小さければ、単位ステップ関数で無視され、
とは直交に近い関係にあるのでこれらの項は小さい。
これが十分小さければ、単位ステップ関数で無視され、
![]() もしくは
もしくは ![]() に近いパターンが出力される。
に近いパターンが出力される。
また、ニューラルネットにおける連想記憶の特徴はつぎのような点である。