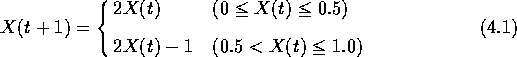
本章では、カオスとカオスアトラクタについての説明をする。
カオス理論の重要性に対する認識は、急速に広まりつつあります。 それに伴って、カオスの乱用も多く見られるようになってきた。 これはある程度仕方のないことでる。 なぜならば、カオスという言葉は誤解を招きやすいし、そもそもカオスをきちんと定義すること自体たいへんチャレンジングな問題であるほど、カオス理論の研究はいまだ未開拓であるからである。
しかしながら、カオスが科学、工学、医学など様々な分野において極めて重要な概念として注目されている。
では、そのカオスについて説明する。
カオス(chaos)とは、決定論に従う力学系の解が初期値に鋭敏に依存する予測不可能な振舞いを示し、そのアトラクタとしての次元が、非線形のフラクタル次元となる現象である。 カオス現象は、自然物、人工物を問わず非線形システムにごくごく当たり前に生じ、風に吹かれて揺れる木の葉や地震の波、海岸にうちよせる波の動きなど日常生活の中にも観察することができる。 もっと身近な例でいえば、ラグビーボールが数回のバウンド後に、突然方向を変える現象を考えるとよい。 またカオスは生体の活動に対しても重要な役割を占めており、例えば心臓の鼓動などがそれにあたる。 心臓の鼓動は常に一定ではなく常に揺らいでおり、刻々と変動していき予測のできない自然の環境の変化に対して一定の鼓動であるよりも柔軟に対応できるようになっている。
カオスの定義は様々な研究者によってなされているが、それらを総じて要約すると、カオスとは、
「決定論的なシステムがつくり出す非周期振動」
では、実際にカオスの例を示す。
式(4.1)は、第 t+1 項X(t+1)の値が第t項X(t)の値によって定まる一般に1次元写像と呼ばれる数列である。
この系の入出力特性は図4.1の様になる。この写像はベルヌーイシフトまたは２進変換と呼ばれる。
カオスの特徴を見るためにこの系に実際に初期値を与えて振舞いを観察してみる。
初期値として0.98765と0.98766を 
として代入し、横軸をt,縦軸をX(t)としてプロットしグラフを描く。
のグラフを図4.2、 
のグラフを図4.3に示す。
この二つのグラフを見ると、始めの数点は似たような振舞いをするが、t=13のあたりから突如振舞いに変化がみられる。
カオスはこのように初期値に鋭敏に反応するという特徴を持つ。
これは図4.1を見ると分かるように、同じX(t+1)を与えるX(t)が二つ存在するため、グラフの平均的な勾配が急で
あるからである。よって非常に近い二つの初期値を持っていたとしてもその振舞いは互いに急に離れていく。 このことは図4.2、図4.3を見ても明らかである。
乱れのないカオスでは、写像と初期値が与えられれば先の値は予測できるため、先ほど述べた初期値鋭敏性はさほど問題ではないが、自然界のような常に乱れの存在する系においては、
小さな乱れであれ鋭敏に反応するため予測ができなくなってしまう。 この（カオス＋小さな乱れ）の系が、 本来は決定論的に定まるカオスを実質的に非決定論的存在にしてしまうのである。
以上のカオスの特徴をまとめると次のようになる。
