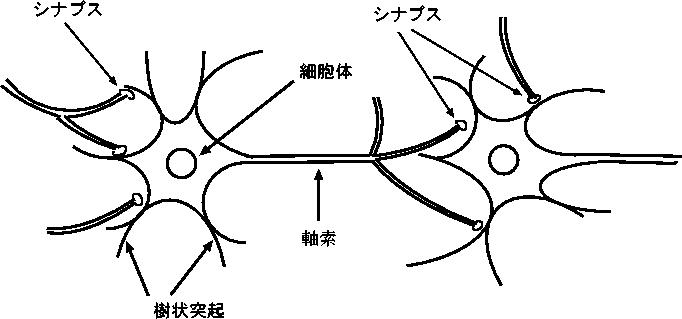
図 2.1: 神経細胞の構造
生体の脳神経系は、外界からの情報を感覚器を介して入力され、脳で情報処理を行ない、さらに効果器を介して外界へ出力されるシステムである。 脳神経系は構造はたいへん複雑であるが、基本的にはニューロン(Neuron:神経細胞)が基本構成要素となっている。概図を図 6.5 に示す。 ニューロンは人間の脳の場合は100億から1000億個程度といわれている。
神経細胞は、細胞体、樹状突起、軸索の3つに分けられる。 細胞の中央部分に当たるのが細胞体であり、タンパク質など細胞の活動に必要な物質はここで生成される。 樹状突起は、細胞体表面から突き出た多くの枝分かれを持った突起をいう。通常、1つの細胞体から数十の樹状突起が出ている。 軸索は枝分かれした末端で、他の神経細胞の細胞体や樹状突起と結合し、ネットワークを形成している。これをシナプス結合という。1つの細胞が受けるシナプス結合の数は、数百ないし数千、まれには数万にもおよぶ。[1]
ニューロンは興奮すると出力側の軸索に電気パルス列を送り出すが、興奮していないときはほとんど出さない。 この電気パルスは1と0に量子化された信号を他のニューロンに送ると考え、興奮状態に送り出される信号を1、非興奮状態に送り出される信号を0とした。 1943年にマッカロ(W.S.McCulloch)とピッツ(W.Pitts)によって提案されたニューロンのモデルを図 6.5 に示す。
この図の ![]() は対象のニューロンの入力の i 番目の結合からの入力であり、
は対象のニューロンの入力の i 番目の結合からの入力であり、 ![]() はその入力と対象ニューロンとのシナプス結合の強さを表す。
はその入力と対象ニューロンとのシナプス結合の強さを表す。
![]() はこのニューロンが持つしきい値であり、ニューロンへと伝わる信号がこれを越えると興奮し、その値以下ならば興奮しない。
yはこのニューロンの出力である。以上のことを表すと下の式になる。
はこのニューロンが持つしきい値であり、ニューロンへと伝わる信号がこれを越えると興奮し、その値以下ならば興奮しない。
yはこのニューロンの出力である。以上のことを表すと下の式になる。
式(2.4) において、 ![]() は i 番目の入力信号を示し、
は i 番目の入力信号を示し、 ![]() はその入力と対象のニューロンとの結合の強さ、また
はその入力と対象のニューロンとの結合の強さ、また ![]() はしきい値を示す。
はしきい値を示す。
![]() の範囲は正から負であり、それぞれ興奮性結合、抑制性結合を表している。
つまり式 (2.4) は、他のニューロンからの荷重和がニューロンに与えられ、それからしきい値を引いたものが u であることを意味している。
の範囲は正から負であり、それぞれ興奮性結合、抑制性結合を表している。
つまり式 (2.4) は、他のニューロンからの荷重和がニューロンに与えられ、それからしきい値を引いたものが u であることを意味している。
f(u) は出力関数である。 この出力関数の取りうる値としては、基本的なものとして2値のみ(0または1)を出力する関数である。これをパーセプトロンという。
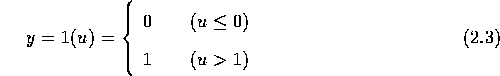
パーセプトロンはニューロコンピュータ研究の原点であるとともに、現在でも基本要素として重要なものである。 これは1961年にローゼンブラッド(Rosenblatt)によって提案された。 さまざまな応用が可能で、学習能力を持つ2値論理関数要素とも見ることができ、実時間信号を処理する適応フィルタ、パターン認識機械とも見ることができる。[2]
また現在、一般的に使われている出力関数はシグモイド関数である。 ここでは、関数 f(u) として
といった形の0〜1までの連続した値をとる図 6.5 のような関数である。 実際の脳の出力にはばらつきがあるため、0か1のステップ関数よりも、このシグモイド関数を用いた方がニューロンの出力関数に適切であるといえる。