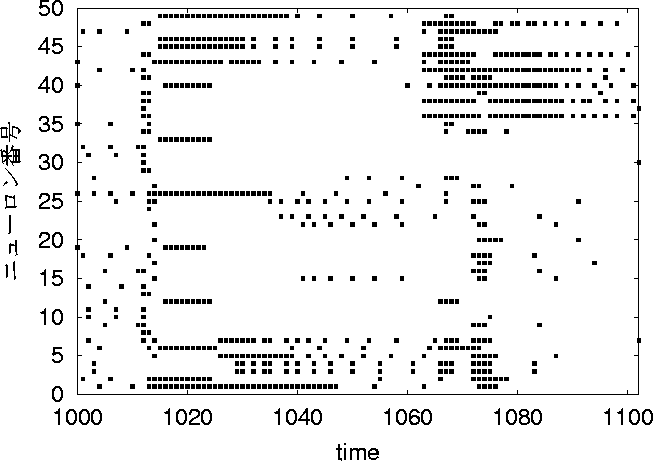
図 4.1: ニューロンの学習状況
学習とはニューロン間のシナプス結合の変化であり,学習するということはそのパターンが入力された時に素早く想起できるようニューロン間のシナプス結合を変化させることである。浅川らが提案した逐次学習法とは,ネットワークを形成する個々のニューロンが単独で自分の内部状態から判断して他のニューロンとの結合荷重を変化させることにより,学習を行なうものである[8]。
図 4.1 はネットワーク内のニューロンの学習状況例で,横軸に時間,縦軸にネットワークを構成しているニューロンを並べている。この図の黒い点はニューロンがその時間に学習をしたことを表している。 本研究で用いたニューラルネットワークの学習において,外部入力は新しい入力パターンに切り替わるまで同じパターンが入力され続ける。この図では時間 1000 , 1050 で外部入力のパターンが切り替わっている。カオスニューラルネットワークは以前の内部状態を残す性質があるために,即座に新しいパターンの学習をすることができない。ここから,ニューロンは新しいパターンを学習する際に若干の時間を要していることが分かる。またこの図から,ニューロンがいっせいに学習することなく単独で学習していることが分かる。
研究で用いたカオスニューロンの内部状態は3つの項(外部入力,相互結合,不応性)の和で決まり,この学習法は相互結合の項が外部入力の項と同じ符合になるよう結合荷重を変化させる。不応性は同じ出力を与えにくくする働きがあり、出力の負のフィードバックをもっている。ここでは不応性の項と同じ大きさまで結合荷重を変化させることで学習を強化させている。またこの過程を多数繰り返すことで,より強固に学習をすることが出来る。学習条件は以下のようになる。
学習条件
この条件式は, 相互結合項 ![]() と 不応性項
と 不応性項 ![]() の和と外部入力
の和と外部入力 ![]() の積が負の時に学習することを表している。
の積が負の時に学習することを表している。
こうして,積が正になるまで結合荷重を変化させ続ける。学習するということは,次にそのパターンが入力された時には,すばやくそのパターンを想起するようにニューロン間の結合荷重を変化させることだからである。
結合荷重の変化は相互結合の項にのみ影響を与える。相互結合の項が外部入力の項と同じ符合になるまで結合荷重を変化させれば,ネットワーク全体のエネルギーの極小点に向かおうとする相互結合の力と,外部入力による入力されたパターンに近付こうとする力が同じ向きに働くようになるため,次にそのパターンが入力された時にはすばやくそのパターンを想起することができるようになる。
式(4.1)が成り立ったニューロンの結合荷重を
次のように変化させる。
i 番目のニューロンの j 番目のニューロンからの
出力に掛かる結合荷重 ![]() の変化は式(4.2)で表される[8]。
i 番目のニューロンの外部入力項と j 番目のニューロンの出力の積が,
正なら結合荷重値を
の変化は式(4.2)で表される[8]。
i 番目のニューロンの外部入力項と j 番目のニューロンの出力の積が,
正なら結合荷重値を ![]() 分加算し,負なら
分加算し,負なら ![]() 分 減算する。
結合荷重値
分 減算する。
結合荷重値 ![]() が正の符合であれば,プラスすることで
j 番目のニューロンとの結合を強め,マイナスすることで弱めることになる。
結合荷重値が負の符合であれば,プラスすることで
j 番目のニューロンとの結合を弱め,マイナスすることで強めることになる。
これを繰り返すことによりネットワークは入力パターンを少しずつ
学習することができる。本研究では,
が正の符合であれば,プラスすることで
j 番目のニューロンとの結合を強め,マイナスすることで弱めることになる。
結合荷重値が負の符合であれば,プラスすることで
j 番目のニューロンとの結合を弱め,マイナスすることで強めることになる。
これを繰り返すことによりネットワークは入力パターンを少しずつ
学習することができる。本研究では, ![]() とした。
とした。