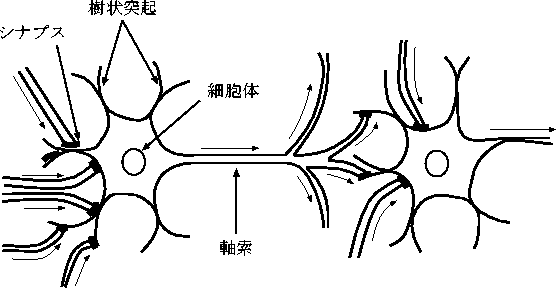
図 2.1: ニューロンの構造
ニューロンとは, 神経細胞のことである。 ニューロンは情報処理用に存在する細胞である。 図 2.1にニューロンの構造を示す。
ニューロンは本体の細胞体の部分と, 複雑に枝分かれした樹状突起と呼ぶ部分, 同じく本体から1本だけ出ていて, 末端で多数に枝分かれする軸索と呼ぶ部分の 三つに分けられる。 軸索とは細胞体本体からの信号を他のニューロンに 伝える出力用の繊維である。 樹状突起は他のニューロンからの信号を受けとる部分である。
枝分かれした軸索の末端部分は, ボタン状の膨らみをつくって 他の神経細胞の細胞体や樹状突起に付着している。 この付着した結合部分をシナプスという。 軸索は十ないし数百に分岐しており, シナプスを介して数多くの細胞につながっている。 また, 1つの細胞が受けるシナプス結合の数は, 数百ないし数千, まれに数万に及ぶ。
通常のニューロン内部の生体電位は, 外部に比べて低いが, シナプス より, 他のニューロンから入力信号を受けとることで, 電位が上がる。 そして, 電位がある大きさ(しきい値)に達すると, ニューロンの内部電位が突然高くなる。 ある大きさとはしきい値を指している。この時, ニューロンは 「発火」又は「興奮」したといい, 軸索にパルス電圧が伝わる。 出力されたパルスは他のニューロンの入力になる。
これはニューロンの最も基本的な性質であり, この性質を用いた ニューロンモデルとして, マッカロ(McCulloch)と ピッツ(Pitts)が提案したものを 図 2.2 に示す。
この図の ![]() は対象となるニューロンの i 番めの入力であり,
は対象となるニューロンの i 番めの入力であり,
![]() は i 番目の入力生体ニューロンのシナプス結合の強さを表す。
は i 番目の入力生体ニューロンのシナプス結合の強さを表す。
![]() は1か0のパルス信号である。
は1か0のパルス信号である。
![]() はこのニューロンに対するしきい値であり,
これを越えると興奮し, 越えなければ興奮しない。
yはこのニューロンの出力である。以上のことをもとにして,
以下の式を導くことができる。
はこのニューロンに対するしきい値であり,
これを越えると興奮し, 越えなければ興奮しない。
yはこのニューロンの出力である。以上のことをもとにして,
以下の式を導くことができる。
式(2.1)において,
![]() は i 番めの入力のシナプス結合の強さを表し,
uを膜電位, もしくは内部ポテンシャルと呼ぶ。
i 番めの入力が来ると(すなわち
は i 番めの入力のシナプス結合の強さを表し,
uを膜電位, もしくは内部ポテンシャルと呼ぶ。
i 番めの入力が来ると(すなわち ![]() )
ニューロンの膜電位が
)
ニューロンの膜電位が ![]() だけ変化することを示す。
だけ変化することを示す。
![]() が正であれば興奮性シナプスを,
負であれば抑制性シナプスを表し, また結合が
なければ
が正であれば興奮性シナプスを,
負であれば抑制性シナプスを表し, また結合が
なければ ![]() である。また式(2.1)の
である。また式(2.1)の
![]() はしきい値を表し,
各入力にシナプスの重みを掛けた荷重和
はしきい値を表し,
各入力にシナプスの重みを掛けた荷重和 ![]() が
しきい値を越えた時のみ, ニューロンが興奮して電気パルスを出力する
(すなわち y=1)離散時間モデルである。
ニューロンモデルは, 一種の多数決で出力を決める素子である。
但し,各入力
が
しきい値を越えた時のみ, ニューロンが興奮して電気パルスを出力する
(すなわち y=1)離散時間モデルである。
ニューロンモデルは, 一種の多数決で出力を決める素子である。
但し,各入力 ![]() の一票の重みは
の一票の重みは ![]() であり,
この一票の格差を積極的に利用するものである。
この際,抑制性のシナプスはマイナスの票を投じることを意味する。
であり,
この一票の格差を積極的に利用するものである。
この際,抑制性のシナプスはマイナスの票を投じることを意味する。
ニューロンモデルの各入力及び出力は, 1又は0の値をとり, 1はニューロンが興奮・発火した状態, 0は静止状態に各々対応する。 この様に, 出力として0, 1の二値をとるようなモデルを, 入力の総和がしきい値を越えた時のみ1を出力することから, 線形しきい値素子モデルという。図2.3にその出力関数を示す。
連続モデルの場合の f(u) の形はいろいろなものが考えられるが, 良く使われるのはシグモイド関数と呼ばれるものである。 シグモイド関数として有名なものは,
という形のものである。