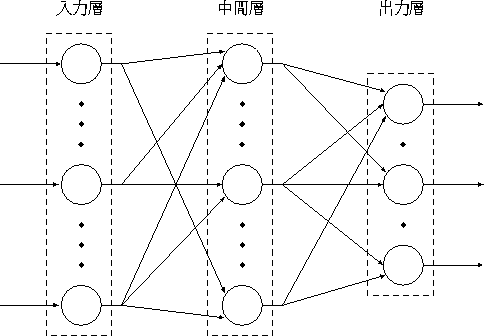
図 3.3: 階層型ネットワーク
続いて、階層型ネットワークを概念的に示すと 図 3.3 のような 構成になる。
このネットワークでは、複数のニューロンがグループ化されて一つの層を形成している と考える。そして、各層は直列に連なって階層を形成するわけである。 ここである層のニューロンは、隣りの層のニューロンのみから情報を受け、 別隣りにある層のニューロンのみへと単方向に情報を送るように結合されている。 つまり、層をまたいだ結合や逆向きに伝わる結合はない。そのため、情報の流れは どこでも一方通行となっており、情報はフィードバックされない。
ネットワークへの入力を扱う初めの層を入力層といい、ネットワークからの 出力を扱う終端の層を出力層という。また、その間の内部にある層を中間層という。
一般に中間層の数が多いほどネットワークの能力は高い。その例として、 中間層の数によるネットワークの線形分離能力の違いを 図 3.4 に示す。 [5]
これは、連続値モデルの普通のニューロンを用いて、二つの入力 x, y と 一つの出力 z をもつネットワークを構築したものである。出力は二つの入力のみに よってきまるので、その動作は3次元空間における曲面 z = f(x,y) で表現できる。 教師信号として0または1を与えて学習させた場合、ネットワーク全体でその曲面を 近似するわけである。
ここで、中間層がないネットワークでは曲面は平面で近似する能力しか持たない。
そのため、出力が1( ![]() 0.5)(色の濃いところ)の部分と0(< 0.5)(白いところ)
の部分との境界は、直線にしかならない。よって、1となる領域が分散している場合など、
典型的な XOR 問題などは解決できないわけである。
0.5)(色の濃いところ)の部分と0(< 0.5)(白いところ)
の部分との境界は、直線にしかならない。よって、1となる領域が分散している場合など、
典型的な XOR 問題などは解決できないわけである。
中間層が一つあれば XOR 問題は解決できるようになるが、まだ噛み合った領域を 分離することはできない。中間層が二つあれば噛み合った領域でさえも分離する ことが可能になり、さらに中間層を増やすことで、より教師信号に忠実な反応が できるようになることは容易に想像できる。
実際には、中間層をいたずらに増やしてもただ無駄になるだけなので、目的に見合った 必要最低限の中間層を設けるわけである。