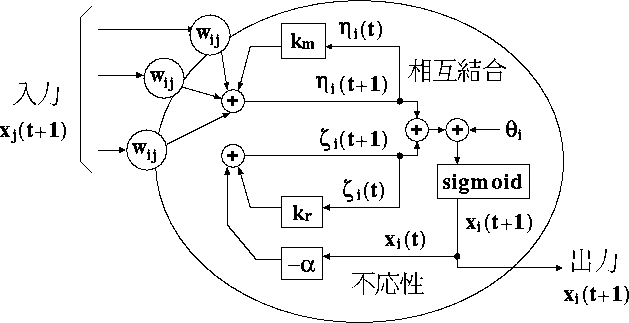
2.3 カオスニューロン

前節で述べた従来のニューロンは、単純でしかも実用的なものとなっており、 多くの応用分野についてそのモデルが使われている。ここでは、ニューロンの動作を 実用範囲内でより忠実にすることを目的として、新たな事象を追加する。すなわち、

• ニューロンが発火した直後は、続けて発火しにくくなる。（不応性）
• 膜電位や不応性の情報は、減衰されながらも少しの期間だけ残る。

の２つの事象である。

合原らはこれらを元に、カオスニューロンのモデル化を行なった。[2] カオスニューロンの特徴は、内部的に過去の情報を記憶していることである。 これによって容易に予測のできない複雑な反応を示す。その内部状態は主に二種類に 分けられる。すなわち、

• 他のニューロンからシナプス結合を通して入力された情報
• 不応性を示すためのニューロンの発火状況を示す情報

である。

彼の示したモデルを実際に使われている形に直し、 それを図 2.5 に示す。

  
図 2.5: カオスニューロン

そして、その動作式を式 (2.5)、式 (2.6)、 式 (2.7) に示す。 、 、 の意味は前節で 説明したものと同じである。その他のパラメータについては追って述べる。

 

  

  

式 (2.6) では、先に述べた内部状態の一方である相互結合入力 を示している。同式の二行目右辺第一項では、単位時間前の 情報 を記憶の減衰定数 km (< 1) 倍して加算することによって、 過去の情報の影響を与えている。そして、第二項によって従来のニューロンモデルと 同じく、他のニューロンからの入力を与えている。

式 (2.7) では、不応性を現すためのもう一方の内部状態である 不応性入力 を示している。同式の二行目右辺第一項では、 先ほどと同じく単位時間前の情報 を記憶の減衰定数 kr (< 1) 倍 して加算することによって、過去の情報の影響を与えている。 そして第二項では、単位時間前の出力 を 倍することによって 不応性の影響を与える。ここで、 は不応性の強さを示す。

これらの情報は閾値 とともに加算され、連続値モデルの代表的な 関数である式 (2.3) のシグモイド関数 を通される。 その結果が、ニューロン i の出力 となる。

これまでに出てきた定数 、 、 がカオスニューロンに特有の 定数であり、これらの値によってカオスニューロンの動作は大きく変わる。 これらもまた、記憶の一部を担っていると考える。