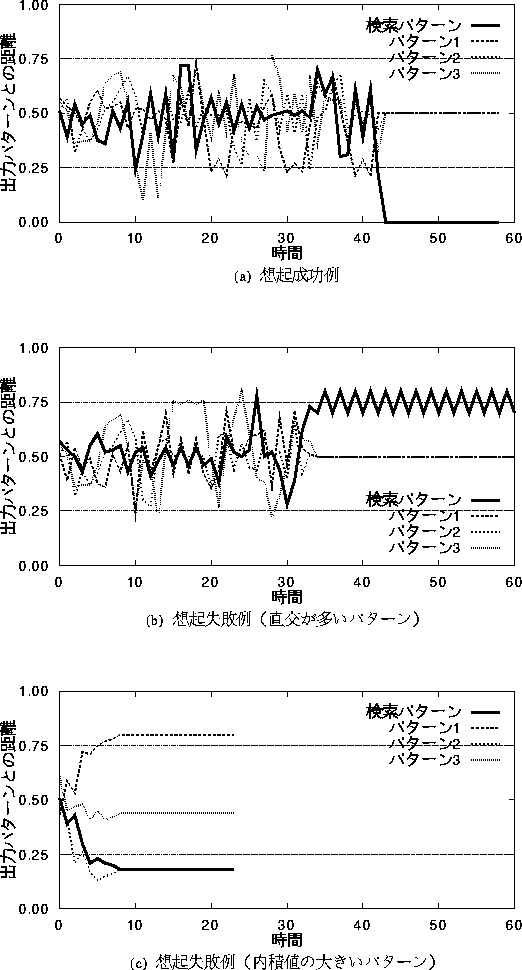
図 8.1: 出力パターンとの距離の時間による変化(成功と失敗の比較)
まず,出力パターンがどのような振舞いをしているかを調べる。 理想的な動作は,第 6.5 節で説明したように,カオス状態の時に, 学習させたパターンをすべて短時間で想起することである。 このように振舞えば,短時間にすべてのパターンに近いものが現れるので, シナプス前抑制によりすべてのパターンが想起可能である。
そこで,学習させたパターンと出力パターンの距離の関係を調べ, 想起できない時の振舞いはどのようになるかを考察し,欠点を追求する。

図 8.1: 出力パターンとの距離の時間による変化(成功と失敗の比較)
図 8.1 は,この距離と時間の関係を求めたものである。 ただし,式 (6.4) のシナプス前抑制関数の しきい値は,前章と同じ gs=0.25 である。
(a) は,想起に成功した時の例である。時間が 10 のとき gs より距離が 小さくなり自己想起状態となったが,パターン 3 を想起しようとしたため, 再びカオス状態へと移っている。最終的には,時間 42 で自己想起状態となり, 43 で想起に成功している。
(b) は,直交の多いパターン(この図のパターンは直交数 5)で, 想起に失敗した例である。時間 30 で gs に近くなっているが,一度も gs を 下回らないので,自己想起状態にならない。 最終的に,検索パターンの反転パターンを想起しようとしているが, カオス状態なので安定せず周期的な振舞いになっている。 つまり,直交するパターンが多いと,自己相関学習の 相互干渉項(式 (5.8) の右辺第 2 項)の影響が小さいので, 自己想起する力が強く 完全なカオス状態にならない。そのため,周期的な振舞いになると考えられる。 または,直交したパターンは,互いの距離が一番はなれているので, 別のパターンとの間の壁(ポテンシャル)が高いため, 一度あるパターンに近付いてから別のパターンへ移ろうとしても, その壁を乗り越えることができない,とも考えられる。
(c) は,内積値がすべて 12 以上で,一度も成功していないパターンである。
ただし,式 (6.5) のカオスニューロンのパラメータが,
このパターンにあっていないために成功しないという可能性があるので,
![]() を次のように変更した。
を次のように変更した。
![]() より
より ![]() が大きい場合は,自己想起を続けることが
わかっている [3] 。そこで,自己想起する力を強くし,
何らかのパターンを想起させるために,
が大きい場合は,自己想起を続けることが
わかっている [3] 。そこで,自己想起する力を強くし,
何らかのパターンを想起させるために, ![]() とした。
このように変更した結果,この図から,時間が 4 で gs より小さくなり,
自己想起状態になって,パターンの距離がすべて一定になっているが,
検索パターンとの距離が 0 になっていないので,
正しいパターンが想起されていないことがわかる。
この出力パターンは,この検索パターンとパターン 2,さらにパターン 1 の
反転パターンが混ざっていると考えられる。
この場合は,(b) とは逆に相互干渉項が大きすぎるため,
正しく学習されていないためか,カオスニューロンに完全なしきい関数(階段関数,
第 5.2.2 節参照)を使用していないためと考えられる。
または,カオスニューロンには,結合荷重の項のみでなく,
その他の項も含んでいるためとも考えられる。
とした。
このように変更した結果,この図から,時間が 4 で gs より小さくなり,
自己想起状態になって,パターンの距離がすべて一定になっているが,
検索パターンとの距離が 0 になっていないので,
正しいパターンが想起されていないことがわかる。
この出力パターンは,この検索パターンとパターン 2,さらにパターン 1 の
反転パターンが混ざっていると考えられる。
この場合は,(b) とは逆に相互干渉項が大きすぎるため,
正しく学習されていないためか,カオスニューロンに完全なしきい関数(階段関数,
第 5.2.2 節参照)を使用していないためと考えられる。
または,カオスニューロンには,結合荷重の項のみでなく,
その他の項も含んでいるためとも考えられる。
次に,成功しやすい条件のパターンでの失敗例である,図 8.2 について 考える。(a) は,通常通り gs=0.25 で行なった結果である。 検索パターンとパターン 3 が重なって, 距離 0.25 の上付近で周期的な振舞いをしている。 つまり,このどちらかのパターンを想起しようとしていると考えられる。 そこで,gs=0.30 とし,自己想起させるようにしたのが (b) である。 しかし,両方のパターンを交互に想起しようとして, 周期的な振舞いなっている。
このように,失敗した例の特徴を見ると,内積値の大きいパターンは, 学習させたパターン以外のものが想起され,それ以外のパターンでは, 自己想起・カオス状態にかかわらず,周期的な振舞いになっている。
次節では,これを改良する方法を考える。