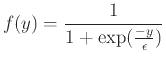カオスニューロンは, ニューロンモデルにカオスを導入したモデルである。
現実でのニューロンに見られる, カオス的な振る舞いをニューロンモデルで再現したモデルで,
合原らによって提唱された。[9]
このモデルはMcCullochとPittsのニューロンモデルでは考慮されなかった,
一度興奮した後,一定期間興奮しなくなる, 興奮しにくくなるといった性質や,
時間とともに電気信号が減衰していく性質を再現している。
カオスニューロンモデルの式は以下のように表される。
![$\displaystyle x(t + 1) = f[A(t) - \alpha \sum_{d=0}^t k^d g\{x(t - d)\} - \theta]$](img27.png) |
(6) |
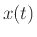 時刻
時刻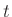 におけるニューロンの出力
におけるニューロンの出力
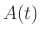 時刻
時刻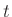 における外部入力の大きさ
における外部入力の大きさ
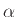 不応性に対する係数
不応性に対する係数
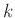 不応性の時間減衰定数
不応性の時間減衰定数
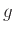 軸索の伝達関数
軸索の伝達関数
不応性は, 一度興奮したニューロンは興奮後, 興奮しにくくなる現象を再現するために設定された性質である。
関数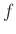 は出力を一定範囲に制限する関数で, 以下のシグモイド関数を用いる。
は出力を一定範囲に制限する関数で, 以下のシグモイド関数を用いる。
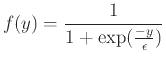 |
(7) |
図 3.2:
Sigmoid function(
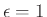 )
)
|
![\includegraphics[height = 8.0cm]{graph6.eps}](img34.png) |
Deguchi Lab.
2017年3月6日
![$\displaystyle x(t + 1) = f[A(t) - \alpha \sum_{d=0}^t k^d g\{x(t - d)\} - \theta]$](img27.png)