ニューロンとは [1, 2]

  ニューロン（neuron）とは、生物の脳を構成する神経細胞のことである。 この神経細胞は、図2.1 のような構成になっており、 核が存在する細胞体、ニューロンの入力である樹状突起、出力部分であるシナプス、 伝送路に当たる軸索がある。 この図では細胞が二個しかないが、人間の脳の場合は およそ100億から1000億程度あるといわれている。

  
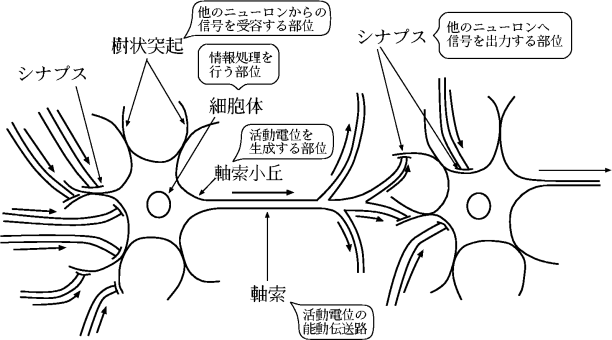
図 2.1: 神経細胞の構造

これらの神経細胞は、立体的に多数集まって回路網を形成している。 一つ一つのニューロンは、他のニューロンから出力を受けとりシナプスで増減し、 それを足した値がある値を超えると出力し、他のニューロンに伝送する。

ニューロンでは、神経インパルス（Nervous Impulse）と呼ばれる 電気パルスを形成し、これが出力となる。 この神経インパルスは神経細胞間で化学反応を介して行なわれるため、 そのパルス幅は、約1[ms]の遅延が生じる。 これは通常のデジタル電子回路に使われるパルスと比べると非常に低速である。 このパルスの振幅は、入力値に関わらずほぼ一定である。しかし 入力は出力に影響しないというわけでなく入力の合計が閾値より小さいと出力せず、 閾値を越えるとパルスを出力する。この特性は、 全か無かの法則（all-or-none law）と呼ばれる。

このニューロンをモデル化したものが、図2.2 である。

  
図 2.2: ニューロンの構造モデル

いま、一つの神経細胞が n 個の細胞から入力を受けているとする。 シナプス前の細胞の出力を 、i番目とj番目のシナプスの結合の強さを と表すと、最も単純には、i番目の細胞からj番目の細胞への影響は と表される。このシナプス結合の強さを、 結合荷重（connection weight）、重みなどと呼ぶ。 結合荷重が正であればそのシナプスは興奮性であり、負であれば抑制性である。 各細胞からの影響が加算されたものが入力になり、これが閾値を超えたときに細胞が「発火」し、出力上で1の値をとる。 これを式で表すと。式(2.1)となる。

 

ここで、 はシグモイド関数であり、m は入力の数、 は i 番目のニューロンの出力、 は i 番目のニューロンから j 番目のニューロンへの重み、 は閾値を表す。 シグモイド関数とは図2.3 に示されるような関数であり、 式(2.2)のように定義される。入力がある値より大きくなった場合 1に近い値を出力し、小さければ0に近い値を出力する。 本来ニューロンは0か1の値しかとらないので階段関数によって実現する方が適切であるが、解析的に問題を解くためにはシグモイド関数のような連続した関数である必要がある。

 

  
図 2.3: シグモイド関数