


Next: 学習
Up: カオスニューラルネットワーク
Previous: カオスニューロンモデル
目次
カオスニューロンによるニューラルネットワークをカオスニューラルネットワークと呼ぶ。
カオスニューロンの入力はネットワーク外部からの入力と、
ネットワーク内部でのフィードバック入力に分けられる。
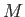 個の外部入力と
個の外部入力と 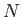 個のニューロン間の相互結合を持つカオスニューラルネットワークの
個のニューロン間の相互結合を持つカオスニューラルネットワークの 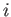 番目のニューロンの振舞いは、
番目のニューロンの振舞いは、
![\begin{displaymath}
\left.
\begin{array}{ll}
x_i(t+1) = & f\biggl[\displayst...
...{t}k_r^d g \{x_i(t-d)\}-\theta_i\biggr]}
\end{array} \right.
\end{displaymath}](img58.png) |
(3.4) |
で表される。
ここで 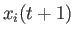 は時刻
は時刻 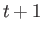 における
における 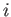 番目のニューロンの出力、
番目のニューロンの出力、
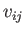 は
は 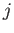 番目の外部入力
番目の外部入力 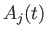 からの
からの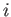 番目のニューロンへの結合係数、
番目のニューロンへの結合係数、
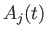 は時刻
は時刻 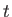 における
における 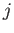 番目の外部入力の大きさ、
番目の外部入力の大きさ、
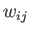 は
は 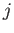 番目のニューロンから
番目のニューロンから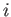 番目のニューロンへの結合荷重、
関数
番目のニューロンへの結合荷重、
関数 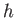 は出力と次の刺激に対する不応性との関係を与える関数、
は出力と次の刺激に対する不応性との関係を与える関数、
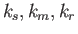 はそれぞれ外部入力、ニューロン間の相互結合、不応性の時間減衰定数である。
はそれぞれ外部入力、ニューロン間の相互結合、不応性の時間減衰定数である。
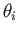 は
は 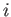 番目のニューロンのしきい値である。
番目のニューロンのしきい値である。
式(3.4) において、外部からの入力を表す項を 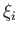 、
ニューロン間の相互結合を表す項を
、
ニューロン間の相互結合を表す項を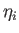 、
ニューロン自身の不応性の項を
、
ニューロン自身の不応性の項を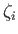 で表し
で表し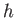 と
と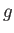 を関数の引数を出力とする恒等関数とするとそれぞれ次のように簡略化することができる。
を関数の引数を出力とする恒等関数とするとそれぞれ次のように簡略化することができる。
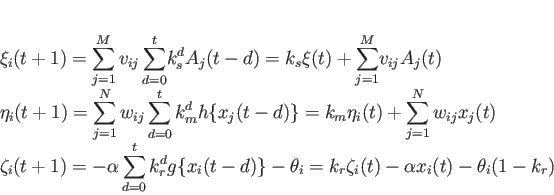 |
(3.5) |
この簡略化したものを用いると 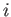 番目のニューロンの出力は次のように表される。
番目のニューロンの出力は次のように表される。
![\begin{displaymath}
x_i(t+1) = f[\xi_i(t+1)+\eta_i(t+1)+\zeta_i(t+1)]
\end{displaymath}](img71.png) |
(3.6) |
式(3.5)と式(3.6)を図に表すと図 3.4 となる。
Deguchi Lab.
2013年2月28日
![]() 個の外部入力と
個の外部入力と ![]() 個のニューロン間の相互結合を持つカオスニューラルネットワークの
個のニューロン間の相互結合を持つカオスニューラルネットワークの ![]() 番目のニューロンの振舞いは、
番目のニューロンの振舞いは、
![]() 、
ニューロン間の相互結合を表す項を
、
ニューロン間の相互結合を表す項を![]() 、
ニューロン自身の不応性の項を
、
ニューロン自身の不応性の項を![]() で表し
で表し![]() と
と![]() を関数の引数を出力とする恒等関数とするとそれぞれ次のように簡略化することができる。
を関数の引数を出力とする恒等関数とするとそれぞれ次のように簡略化することができる。
![]() 番目のニューロンの出力は次のように表される。
番目のニューロンの出力は次のように表される。