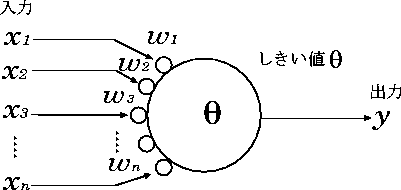
図 2.2: ニューロンモデル
今、図 2.2 のように1つの神経細胞が n 個の細胞から
入力を受けているとする。
シナプス前細胞の出力を ![]() 、
それぞれのシナプスの結合の強さを
、
それぞれのシナプスの結合の強さを ![]() と表すと、
i 番目の細胞からの影響は、
と表すと、
i 番目の細胞からの影響は、 ![]()
![]() と表される。
このシナプス結合の強さを結合荷重と呼ぶ。
と表される。
このシナプス結合の強さを結合荷重と呼ぶ。
そして、各細胞からの影響 ![]()
![]() を加算したもの
(
を加算したもの
( ![]()
![]() )が細胞の入力になり、
この和がしきい値
)が細胞の入力になり、
この和がしきい値 ![]() を越えた時に細胞が興奮する。
さらに軸索は減衰のない伝送路であると仮定すれば、
このようにして生じた興奮がその細胞の出力になる。
を越えた時に細胞が興奮する。
さらに軸索は減衰のない伝送路であると仮定すれば、
このようにして生じた興奮がその細胞の出力になる。
以上の説明を式で表すと、式(2.1),(2.2)のように まとめられる。
式(2.1) は、他の細胞からの荷重が細胞に与えられ、 それからしきい値を引いたものが u であることを意味している。 この u を膜電位、もしくは内部ポテンシャルと呼ぶ。 また式(2.2) は、細胞の出力は膜電位 u の関数として 決まることを表している。
入力 ![]() 、出力 y の取りうる値としては、2値(0,1)のみを許す
モデルや実数値を許すモデルがある。
マッカロとピッツのモデルは2値モデルであり、
関数 f(u) は式(2.3) で定義される階段関数になる。
、出力 y の取りうる値としては、2値(0,1)のみを許す
モデルや実数値を許すモデルがある。
マッカロとピッツのモデルは2値モデルであり、
関数 f(u) は式(2.3) で定義される階段関数になる。
このように、出力として0,1の2値をとるようなモデルを、
入力の線形和( ![]()
![]() )がしきい値(
)がしきい値( ![]() )を越えた時のみ
1を出力することから、特に「線形しきい値素子」モデルという。
)を越えた時のみ
1を出力することから、特に「線形しきい値素子」モデルという。
連続値形モデルの場合 f(u) の形はいろいろなものが考えられるが、 よく使われるものに図 2.3 のような シグモイド関数と呼ばれるものがある。 シグモイド関数として代表的なものは、式(2.4) である。