確率的潜在意味解析 [10]

確率的潜在意味解析（Probabilistic Latent Semantic Analysis：以下PLSA）はT. Hofmann氏によって考案された、LSAや要素解析に対するアプローチの１つである。これはアスペクトモデルと呼ばれる統計モデルを中心とし、LSAにはない確率的な変数を用いることで、統計的根拠に基づいた手法であるとされている。Hofmann氏の書いた論文[10]によれば、LSAだけでなく $tf \mathchar\lq - idf$法などの直接用語の一致を見る方法をも凌ぐ有用さが示されており、多義語や類義語さえも扱えるとされている。以下にこのPLSAの内容について説明する。

まずアスペクトモデルは、文書 $d \in D = \{d_{1}, \ldots d_{N}\}$中に存在する単語 $w \in W = \{w_{1}, \ldots w_{M}\}$に伴う隠れ（非観測）変数 $z \in Z = \{z_{1}, \ldots z_{K}\}$に関する潜在変数モデルを指し、これを生成モデルを用いて表現すると、以下のように定義することが出来る。

• 確率$P(d)$により文書$d$が選択される。
• 確率$P(z \, \vert \,d)$により隠れ変数$z$が選択される。
• 確率$P(w \, \vert \,z)$により単語$w$が生成される。

この結果により観測データ$(d, w)$の組が得られ、その過程で$z$は破棄されることになる。これを結合確率モデルで表すと、次式のようになる。

$$P(d, w) = P(d)P(w \, \vert \,d)$$ (3.17)

$$P(w \, \vert \,d) = \sum_{z \in Z} P(w \, \vert \,z)P(z \, \vert \,d)$$ (3.18)

式(3.18)から分かるように、これはある観測データを引き起こした全ての隠れ変数を考慮しなければならない。また文書中の語句の分布$P(w \, \vert \,d)$は$P(w \, \vert \,z)$の凸結合から得られ、文書はクラスタに割り当てられずに、重み$P(z \, \vert \,d)$によって特徴づけられる。この重みは、クラスタモデルや教師無しの単純なベイズモデルによる事後確率とは大きく異なり、概念的でモデルとして優れているとHofmann氏は述べている。

ここで$P(z)$, $P(z \, \vert \,d)$, $P(w \, \vert \,z)$は尤度原理に従うことで、以下の対数尤度関数を最大化することよって決定される。

$$L = \sum_{d \in D} \sum_{w \in W} n(d, w) \log P(d, w)$$ (3.19)

なお、この式において$n(d, w)$は用語頻度、すなわち文書$d$中に単語$w$がいくつ存在するかを表す。ここで、ベイズの定理[11]を用いて条件付き確率$P(z \, \vert \,d)$を反転させると、以下のようになる。

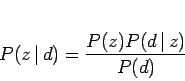$$P(z \, \vert \,d) = \frac {P(z)P(d \, \vert \,z)} {P(d)}$$ (3.20)

これと式(3.17), 式(3.18)により以下の等価なモデルが得られ、実際の計算にはこの式を利用することになる。

$$P(d, w) = \sum_{z \in Z} P(z)P(w \, \vert \,z)P(d \, \vert \,z)$$ (3.21)

より適切な計算結果を得る為には式(3.19)を最大化する必要があり、これを見積もる手続きとして、EM（Expectation Maximization）アルゴリズムが用いられる。このアルゴリズムの特徴としては、尤度が単調増加することが保証されており、初期段階の速度がニュートン法と同程度であることが知られている。その中身は２つのステップに分かれており、１つ目のEステップは$P(z)$を始めとする現在のパラメータを見積もり、$z$によって事後確率を計算する。２つ目のMステップはEステップによって計算された事後確率により、パラメータを更新する。ここで再びベイズの定理を用いてEステップを導くと、次に示す式が求まる。

$$P(z \, \vert \,d, w) = \frac {P(z)P(d \, \vert \,z)P(w \, ... ...t \,z)} {\sum_{z'} P(z')P(d \, \vert \,z')P(w \, \vert \,z')}$$ (3.22)

これは観測データの発生が隠れ変数によって説明されることを示しており、計算を進めることで以下のパラメータ更新に関するMステップの方程式が得られる。

$$P(w \, \vert \,z) = \frac {\sum_{d} n(d, w)P(z \, \vert \,d, w)} {\sum_{d, w'} n(d, w')P(z \, \vert \,d, w')}$$ (3.23)

$$P(d \, \vert \,z) = \frac {\sum_{w} n(d, w)P(z \, \vert \,d, w)} {\sum_{d', w} n(d', w)P(z \, \vert \,d', w)}$$ (3.24)

$$P(z) = \frac {1} {R} \sum_{d, w} n(d, w)P(z \, \vert \,d, w)$$ (3.25)

$$R \equiv \sum_{d, w} n(d, w)$$

この式(3.22) $sim$ 式(3.25)までの収束手続きを繰り返すことで、式(3.19)に示す対数尤度関数の局所的最大値に近づくことが出来る。尤度を最大化することは語句の複雑さを減少させることと等価であり、これにより文書あるいは単語の繋がりを見つけやすくなる。この為、より尤度を高める為に、このEMアルゴリズムを改良した手法であるTEM（tempered EM）が提唱されている。これは決定論的焼きなまし法に非常に近く、エントロピー的な要素を取り入れたアルゴリズムである。具体的には式(3.22)に温度の逆数を表す$\beta$を導入して修正を加えたものであり、これは以下の式で表される。

$$P_{\beta} (z \, \vert \,d, w) = \frac {P(z)[P(d \, \vert \... ...{\sum_{z'} P(z')[P(d \, \vert \,z')P(w \, \vert \,z')]^\beta}$$ (3.26)

ここで$\beta = 1$の時は標準のEステップとなるが、$\beta < 1$の時はベイズの定理に関する部分だけが対数的に増加することになる。この$\beta$は尤度の増加が見られなければ $\beta = \eta \beta \, (\eta < 1)$によって徐々に減少させ、これによってTEMは収束アルゴリズムを定義し、過剰適合を回避出来るという利点を持つことになる。このように焼きなまし法の主旨に多少反するが、温度の上昇によりデータを鍛える（temper）というのがこのTEMの特徴である。

PLSAの問題点としては確率的な変数を用いる為に初期値依存性があることで、これによって大きく結果が変わることがある。また、隠れ変数の数や反復回数、$\beta$を減少させる時の係数である$\eta$などのパラメータを上手く決定する必要があり、ここがLSAにはないデメリットとなっている。