状態変数と状態方程式

図２．１で与えられるシステムを考える。このシステムに対し、入力を$u(t)$，出力を$y(t)$とすると、運動方程式は次式で与えられる：

$$m \ddot{y}(t) + d \dot{y}(t) + ky(t) = u(t).$$ (1.1)

上式は出力$y(t)$から入力$u(t)$を特徴付ける式であることが判るが、 一般に与えられたシステムを思い通りに制御するには入力から出力を特徴付ける 必要がある。

このため古典制御理論では、(1.1)式をラプラス変換し、単純な代数方程式に することで入力から出力を求めている。具体的には(1.1)式に対し，初期条件 $y(0)=0, u(0)=0$を適用し，ラプラス変換すると

$$m s^2 Y(s) + d s Y(s) + k Y(s) = U(s)$$ (1.2)

が得られ、これから入力$U(s)$と出力$Y(s)$との比 $Y(s)/U(s)=G(s)$を求めることで入力と出力の関係を導き出している。

しかし、このように与えられたシステムの微分方程式をラプラス変換により簡単化するためには、システムが１入力１出力であることが要求され、より複雑なシステムに対しては、古典制御理論では十分でないことが判る。

現代制御理論は、上記のような古典制御理論の不備を補うため、状態変数というものを導入し、システムを状態方程式と呼ばれる１階の行列微分方程式で記述する手法を確立した。実際、(1.1)式で与えられるシステムを状態方程式により記述してみる。 そのため、次式のように新しい変数$x_1(t),x_2(t)$を導入する：

$$\left\{ \begin{array}{l} x_1(t) = y(t),\\ x_2(t) = \dot{y}(t). \end{array}\right.$$ (1.3)

明らかに(1.3)式より

$$\dot{x}_1(t) = x_2(t), \quad \dot{x}(t) = \ddot{y}(t).$$ (1.4)

また、(1.3),(1.4)式を(1.1)式に代入すると

$$m \dot{x}_2(t) + d x_2(t) + k x_1(t) = u(t)$$

となり、$\dot{x}_2(t)$について整理すれば

$$\dot{x}_2(t) = -\frac{d}{m}x_2(t) - \frac{k}{m}x_1(t) + \frac{1}{m}u(t)$$ (1.5)

となる．(1.4)式と(1.5)式をまとめると

$$\left[ \begin{array}{c} \dot{x}_1(t) \dot{x}_2(t) \end{ar... ...] + \left[ \begin{array}{c} 0 1/m \end{array} \right] u(t)$$ (1.6)

となり、さらに状態ベクトルとして$x(t)$を

$$x(t) = \left[ \begin{array}{c} x_1(t) x_2(t) \end{array} \right],$$

行列$A$，ベクトル$b,c$をそれぞれ

$$\left[ \begin{array}{cc} 0 & 1 -k/m & -d/m \end{array} \r... ...ght], \quad \left[ \begin{array}{cc} 1 & 0 \end{array} \right]$$

で定義すれば(1.6)式は

$$\dot{x}(t) = Ax(t) + bu(t)$$ (1.7)

$$y(t) = cx(t)$$ (1.8)

となる。

さらに，図2.1で与えられるシステムを別の状態変数を使って表現することもできる． 実際次のように状態変数$x_1(t)$,$x_2(t)$を定めるとする：

$$x_1(t) = \dot{y}(t) + \frac{d}{m}y(t), \quad x_2(t) = y(t).$$

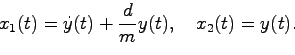
このときシステムの状態方程式は次式で与えられる：

$$\begin{eqnarray*} \dot{x}(t) &=& \left[ \begin{array}{cc} 0 & -k/m 1 & -d/m \... ...(t) &=& \left[ \begin{array}{cc} 0 & 1 \end{array}\right] x(t). \end{eqnarray*}$$

このことは，システムの状態方程式表現は１つではなく，状態変数の取り方により いろいろな状態方程式を考えることを示している．

次に電気系の例を考える． 図2.2で与えられる回路を考える．端子電圧$v_i(t)$を入力，$v_o(t)$を出力とすると， キルヒホッフの法則により，閉路1については

$$v_o(t) = v_i(t) - Ri(t)$$

が成り立ち，閉路2については

$$Cv_o(t) = \int_0^t i(\tau) d\tau$$

が成り立つ．したがって，

$$R C \dot{v}_o(t) + v_o(t) = v_i(t)$$

となり，さらに状態変数を$x(t)=v_o(t)$，入力を$u(t)=v_i(t)$，出力を$y(t)=v_o(t)$とすれば，この系の状態方程式表現は

$$\begin{eqnarray*} \dot{x}(t) &=& -\frac{1}{RC}x(t) + \frac{1}{RC}u(t), \\ y(t) &=& x(t) \end{eqnarray*}$$

となる．

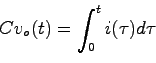
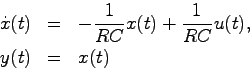
これらの例では，入力$u(t)$も出力$y(t)$も共にスカラーであったが，現実には１つのシステムに複数個の入力と出力を持つことが考えられる．このため，状態方程式(1.7),(1.8)式を，上記のような多入力多出力の場合にまで一般化すると

$$\dot{x}(t) = Ax(t) + Bu(t)$$ (1.9)

$$y(t) = Cx(t)$$ (1.10)

となる．ただし，$x(t)$は$n$次元状態ベクトル，$u(t)$は$m$次元入力ベクトル，$y$は$r$次元出力ベクトルであり，$A,B,C$はそれぞれ $n \times n,n \times m, r \times n$の（定数）行列である．さらにこのシステムをブロック線図で表すと図2.3のようになる．

例2.2　多入力多出力システムの例として，図2.4の力学系を挙げる．ここで$m_1,m_2$はそれぞれ物体Aと物体Bの質量，$k$をバネ定数，$d$をダッシュポットの減衰定数とする．さらに，物体Aと物体Bにはそれぞれ任意の力$u_1(t),u_2(t)$を加えることができるものとする．このとき物体A，物体Bがある平衡状態$y_{1s},y_{2s}$に対し，どれだけ位置が変化するかを$y_1(t),y_2(t)$により表し，これら$y_1(t),y_2(t)$を制御することを考える．

システムの運動方程式は以下で与えられる：

$$\begin{eqnarray*} m_1 \ddot{y}_1(t) &=& k(y_2(t)-y_1(t)) + d(\dot{y}_2(t)-\dot{y... ...&=& -k(y_2(t)-y_1(t)) - d(\dot{y}_2(t) - \dot{y}_1(t)) + u_2(t). \end{eqnarray*}$$

(1.11)式の$\ddot{y}_1$及び(1.11)式の$\ddot{y}_2$に注目し， 状態ベクトル$x(t)$を

$$x(t) = \left[ \begin{array}{cccc} y_1(t) & \dot{y}_1(t) & y_2(t) & \dot{y}_2(t) \end{array}\right]^T,$$

入力ベクトル$u(t)$を

$$u(t) = \left[ \begin{array}{cc} u_1(t) & u_2(t) \end{array}\right]^T,$$

出力ベクトル$y(t)$を

$$y(t) = \left[ \begin{array}{cc} y_1(t) & y_2(t) \end{array}\right].$$

とすると，(1.11),(1.11)式及び $\dot{x}_1(t)=x_2(t)$, $\dot{x}_3(t)=x_4(t)$ より

$$\begin{eqnarray*} \dot{x}(t) &=& \left[ \begin{array}{cccc} 0 & 1 & 0 & 0 \\ -k... ...rray}{cccc}1 & 0 & 0 & 0 0 & 0 & 1 & 0 \end{array}\right]x(t) \end{eqnarray*}$$

となる．